Para acompanhar o roteiro é importante ter uma compreensão básica de análises estatísticas em R, partimos da premissa que você já sabe interpretar o resumo de um modelo linear usando as funções como lm() e summary(). Como os modelos mistos ainda não foram incorporados na interface do Rcdmr, será preciso rodar no R os códigos que aparecem em caixas de textos nesse roteiro.

 cat("Isso é um código do R") 

Para isso, cole as linhas de texto na janela superior do Rcmdr e clique no botão Submite (ou Submeter) para executar a linha em que o cursor do mouse se encontra, ou selecione um conjunto de linhas para executá-las juntas. É possível rodar os códigos a partir de um console básico do R também. Caso queira usar um escript direto no R veja o tutorial Introdução ao R

O objetivo desse roteiro e que você seja capaz de:

Para auxiliar a entender terminologias estatísticas específicas, ou caso queira relembrar alguns termos, ao final do roteiro encontra-se um pequeno glossário.

pkgs <- c("lme4", "RVAideMemoire")
pkgsNot <- pkgs[!(pkgs %in% rownames(installed.packages()))]
install.packages(pkgsNot)

Para explicar o que são modelos mistos e sua importância em ecologia, usaremos como exemplo um conjunto de dados presente no capítulo 5 de Zuur et al. (2009). Esses dados contêm a riqueza de espécies da macro-fauna em 9 praias na costa da Holanda. Em cada uma das praias, os autores coletaram dados em cinco localidades diferentes. Para cada localidade existe informação sobre a altura da estação de amostragem em relação à altura média da maré (NAP, variável contínua) e também um índice de exposição da praia (Exposure, variável categórica).

Vamos supor que estamos interessados em verificar se a variável NAP influencia a riqueza de espécies nessas praias, deixando de lado a variável de exposição por hora. Podemos, por exemplo, construir um modelo linear da seguinte forma:

$$riqueza = \alpha + \beta * NAP + \varepsilon$$

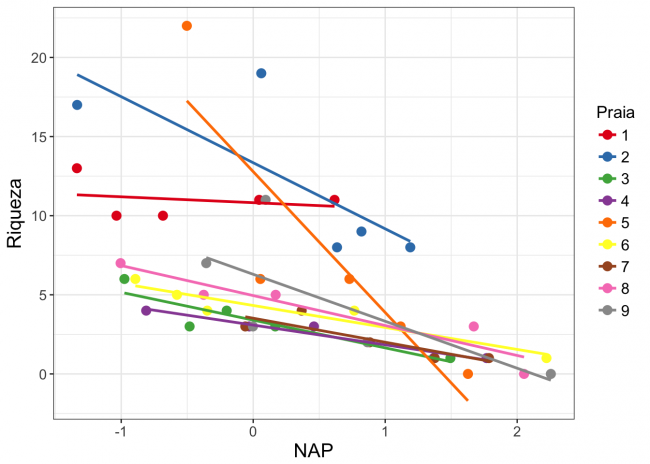
Aqui estamos modelando a riqueza de cada ponto de amostra em função da variável NAP. O coeficiente $\alpha$ é o intercepto do modelo, $\beta$ é o coeficiente angular (inclinação) de NAP e $\varepsilon$ é o erro do nosso modelo (resíduos), isto é, a variação da riqueza que não conseguimos explicar com nossa variável preditora NAP. No entanto, esse modelo tem um problema sério. Estamos violando uma premissa fundamental de modelos lineares, a de que os dados são independentes uns dos outros (Winter, 2013). Os dados obtidos em uma mesma praia não são independentes entre si (dependência espacial). Podemos imaginar diversas características de cada praia que podem influenciar a riqueza de espécies, como o tipo de grão de areia ou a força das ondas, que não estão contempladas em nosso modelo e podem fazer com que as amostras de uma mesma praia sejam mais parecidas, independente das nossas variáveis de interesse ( no caso apenas NAP). Veja o gráfico abaixo, em que cada cor representa uma praia, para se convencer de que a relação entre riqueza e NAP varia entre praias:

Nesta figura, temos as retas do modelo entre Riqueza e NAP aplicado para cada praia (usando a função lm()). Entretanto, nossa pergunta inicial não diz respeito a cada praia separadamente, nós queremos modelar esta relação para todas as praias amostradas, sem especificar a relação para cada praia. A inclusão de unidades amostrais que apresentam dependência entre elas é chamada de pseudo-replicação ou falta de independência das observações. Queremos considerar essa dependência sem falar especificamente de nenhuma praia e, ao mesmo tempo, ser possível ter alguma ideia da variação que existem entre as praias, inclusive as que não foram amostradas.

Para isso, precisamos de um modelo linear que incorpore o fato de que nossos dados estão agrupados em praias. Chamamos de efeito aleatório uma variável que agrupa nossos dados e que, geralmente, seu efeito sobre a variável resposta não nos interessa diretamente (nesse exemplo não interessa, mas dependendo da análise, pode interessar - veja discussão em McGill 2015). Nesse exemplo, os autores amostraram nestas 9 praias, mas poderiam ter feito o mesmo estudo escolhendo outras praias. O efeito aleatório praia organiza parte da variação nos nossos dados que não conseguimos explicar, presente no erro $\varepsilon$ do modelo simples descrito no início desse roteiro (Winter, 2013). Por outro lado, as variáveis preditoras que estamos acostumados a encontrar em modelos lineares são chamadas de aqui de efeitos fixos. No exemplo das praias, a variável NAP é um efeito fixo e estamos diretamente interessados em seu efeito sobre a variável resposta. O nome misto refere-se ao fato de que existirem efeitos fixos e aleatórios no modelo. Esses modelos são chamados também de hierárquico ou multinível.

Em ecologia, é comum encontrarmos delineamentos amostrais ou experimentais que geram dados com algum tipo de agrupamento (delineamento hierárquico ou aninhado). Por exemplo, quando uma amostragem é feita por parcelas ou quando um experimento é separado em diferentes blocos. Nesses casos, não podemos tratar nossos dados como independentes e a abordagem estatística mais adequada é a de modelos mistos.

Na seção a seguir veremos como explorar modelos mistos no R. Veremos que a forma mais simples de incorporar o efeito aleatório em nosso exemplo é definir que cada praia apresenta um intercepto diferente no modelo. Ou seja, queremos ajustar uma reta para nossa relação entre riqueza e NAP, mas permitir que cada praia tenha seu próprio intercepto, que é relacionado ao intercepto da reta principal (efeito fixo).

Nosso modelo será:

$$riqueza_i = \alpha + b_i + \beta * NAP + \varepsilon_{i}$$

sendo:

$$b_i ~ N(0, \sigma_{praia})$$

$$ \varepsilon ~ N(0, \sigma_{res})$$

A riqueza da praia i é explicada pelo efeito fixo $\beta*NAP$ e pelo efeito aleatório $b_i$, que se soma ao valor do intercepto fixo do modelo, $\alpha$, para formar o intercepto da praia i. Veja que o índice i está atrelado a $b_i$ e, portanto, o modelo permite que cada uma das praias apresente um intercepto diferente, mas mesmas inclinações $\beta$. O $\beta$ faz parte do efeito fixo, e não possuí nenhum índice i atrelado a ele, portanto é o mesmo para todas as praias. Finalmente, $\varepsilon$ representa o resíduo associado ao desvio do valor observados em relação ao predito pela reta da praia relativa à observação.

Existem vários pacotes disponíveis no R para realizar análises de modelos mistos. Neste roteiro usaremos o lme4 (Bates et al. 2014), que possui funções para analisar modelos lineares mistos, modelos lineares mistos generalizados e modelos mistos não lineares. A seguir, vamos colocar a mão na massa e analisar os dados provenientes do capítulo 5 de Zuur et al. (2009) que exploramos na seção anterior.

Antes de tudo, precisamos baixar e instalar o pacote lme4:

##caso não tenha instalado o pacote tire o comentário da linha seguinte
#install.packages("lme4")
library(lme4)

Os dados estão disponíveis no site do livro do Zuur et al. (2009)¹⁾, mas podem ser baixados no link abaixo.

• baixe o arquivo dados vamos à praia
• no R, mude o diretório de trabalho (pasta) para o diretório onde o dado se encontra
• leia os dados praia.txt com o seguinte comando ²⁾
• o arquivo é do tipo texto, com colunas separadas por tabulação (“Tabs”) e com decimal indicado por ponto (“.”)

dados <- read.table("praia.txt", header = TRUE, sep = "\t" , as.is = TRUE)
head(dados) #observando as primeiras linhas de dados
str(dados) # vendo se a estrutura dos dados está ok!

Aqui vamos apenas transformar a variável fExp em fator com dois níveis (low, high), nesta ordem, criando uma nova variável fExposure

dados$fExposure <- factor(dados$fExp, levels = c("low", "high"))

Agora, vamos construir nosso modelo. Relembrando, estamos interessados em ver se existe um efeito de NAP na riqueza de espécies. Nossos dados contam com nove diferentes praias e cinco diferentes amostras para cada uma delas. Dessa forma, temos como efeito fixo a variável NAP, e como efeito aleatório a variável praia (Beach'), que significa que cada praia terá um intercepto diferente. Assim, nosso modelo é:

modelo.riqueza <- lmer(Richness ~ NAP +  (1 | Beach), data = dados)

Em seguida, vamos dar uma olhada no output do modelo:

A função summary aplicada a um objeto de modelos, retorna as informações mais relevantes do mesmo.

summary(modelo.riqueza)

Vamos dar uma olhada na parte dos efeitos aleatórios (Random effects). O desvio padrão (Std.Dev.) é uma medida do quanto a variabilidade da nossa variável dependente - riqueza - é devida aos dois efeitos aleatórios que estamos analisando (os interceptos das praias e os resíduos). Podemos ver o desvio padrão associado às diferenças de intercepto entre praias (o $b_i$ do modelo). A última linha nos dá o resíduo, que indica o quanto da variabilidade não é prevista pela variável aleatória praia nem pelo NAP, que nada mais é do que o $\varepsilon$ acima explicado.

Os efeitos fixos indicam os coeficientes estimado pra cada um dos fatores que estamos considerando como fixos. No caso, temos o intercepto (medio de todas as praias) que é a riqueza quando o NAP é zero (6.5819), e o coeficiente angular de NAP (-2.5684), o que indica que há uma diminuição de riqueza da ordem de mais de 2.5 espécies a cada unidade de NAP acrescida.

#criando objeto com os coeficientes do modelo (efeitos fixos)
fixLMM <- fixef(modelo.riqueza)
fixLMM

Além desses coeficientes, os modelos mistos também fazem a estimativa aproximada para cada um dos níveis da variável aleatória e que pode ser acessado da saguinte forma:

#criando objeto com os coeficientes do modelo (efeitos fixos)
randLMM <- coef(modelo.riqueza)
randMM

Note que a inclinação é a mesma para todas as praias e o intercepto médio dos coeficientes da estrutura aleatória do modelo é o intercepto da estrutura fixa.

mean(randMM[,1])

Para fazer o gráfico de nosso modelo ajustado, com a reta média predita pela estrutura fixa do modelo e as retas da estrutura aleatória, preditas para cada praia, vamos primeiro calcular os valores preditos para cada praia.

O predito pelo modelo pode ser calculado a partir dos coeficientes. Como a intenção é construir uma curva, utilizamos uma sequência de valores da preditora (variável no eixo x, no caso NAP) e estimamos valores em intervalos curtos para podermos construir a curva do modelo.

seqNAP <- seq(-1.5, 2.5,len=100)
beach01 <- randLMM[1,1] + randLMM[1,2] * seqNAP
beach02 <- randLMM[2,1] + randLMM[2,2] * seqNAP
beach03 <- randLMM[3,1] + randLMM[3,2] * seqNAP
beach04 <- randLMM[4,1] + randLMM[4,2] * seqNAP
beach05 <- randLMM[5,1] + randLMM[5,2] * seqNAP
beach06 <- randLMM[6,1] + randLMM[6,2] * seqNAP
beach07 <- randLMM[7,1] + randLMM[7,2] * seqNAP
beach08 <- randLMM[8,1] + randLMM[8,2] * seqNAP
beach09 <- randLMM[9,1] + randLMM[9,2] * seqNAP
beachFix <- fixLMM[1] + fixLMM[2] * seqNAP

Vamos primeiro construir um gráfico base, com os valores observados. Para tornar o gráfico mais informativo vamos colocar cores para identificar de que praia a observação foi coletada. No código abaixo temos as seguintes sequencia de eventos:

• cores…: cria um objeto com nove cores tiradas de uma paleta das cores do arco-iris
• par(…) : modifica parâmetros da janela gráfica, no caso modificamos as bordas
• plot(…): cria o gráfico
  • 1° linha: os dados
  • 2° e 3° linha: modificações de parâmetros do gráfico

cores <- rainbow(9)
par( mar=c(5,5,2,2))
plot(Richness ~ NAP ,data = dados,
     pch = 19, col = cores[as.factor(Beach)] , las = 1,
     cex=1.5, cex.lab= 1.7, cex.axis = 1.5
     )

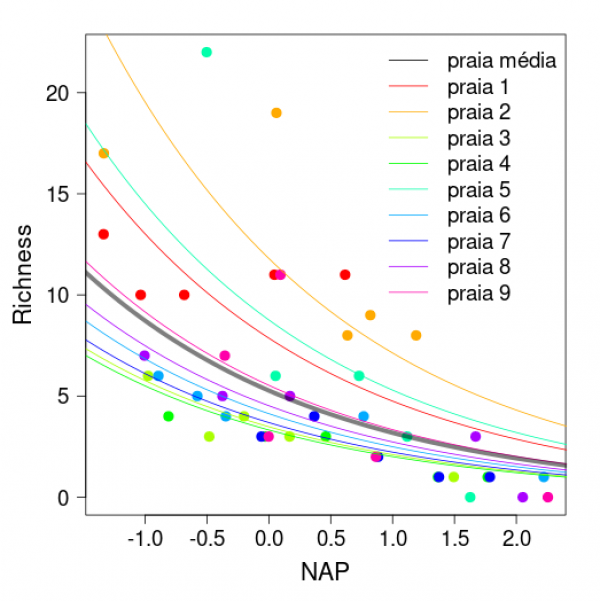
Vamos usar os valores que calculamos para representar as esperanças do modelo e criar as curvas para cada praia e a curva média. No cṕdigo abaixo as primeiras linhas incluem as curvas associadas a cada uma das praias amostradas, a penultima linha inclui o predito pela estrutura fixa do modelo e a última a legenda.

lines(beach01a ~ seqNAP, col = cores[1])
lines(beach02a ~ seqNAP, col = cores[2])
lines(beach03a ~ seqNAP, col = cores[3])
lines(beach04a ~ seqNAP, col = cores[4])
lines(beach05a ~ seqNAP, col = cores[5])
lines(beach06a ~ seqNAP, col = cores[6])
lines(beach07a ~ seqNAP, col = cores[7])
lines(beach08a ~ seqNAP, col = cores[8])
lines(beach09a ~ seqNAP, col = cores[9])
lines(beachFixa ~ seqNAP, col = rgb(0,0,0,0.5), lwd=5)
legend("topright", c( "praia média",paste("praia", 1:9)) , lty=1, col= c(1,cores), bty="n", cex=1.5)

Podemos ver nessa figura a predição do nosso modelo em relação aos parâmetros fixos (reta em preto), e as predições para cada praia separadamente. Como o efeito aleatório do nosso modelo estava apenas variando os valores de intercepto das praias, as retas para cada praia são paralelas.

Existem, entretanto, diversas maneiras de criar seu modelo, escolher os parâmetros importantes, e decidir quais são fixos e quais são aleatórios. Nesse exemplo, poderíamos colocar a variável `Exposure` também como um efeito fixo. Outra complicação que poderíamos inserir no nosso modelo é inserir mais um efeito aleatório de interação entre a praia (efeito aleatório) e NAP (efeito fixo), fazendo com que cada praia possa também ter sua relação com a NAP (inclinações de reta diferentes).

Por isso, é importante testar diferentes modelos antes de decidir qual é o melhor. Na próxima parte abordaremos como selecionar o melhor modelo dadas todas as possibilidades.

Existem modelos e, portanto, perguntas e delineamentos amostrais, que requerem apenas um efeito aleatório para indicar o agrupamento dos dados. Entretanto, como colocado no final da seção anterior, há também modelos que podem incluir mais de um efeito aleatório. Esse é o caso da interação entre praia e NAP mencionada acima. Se olharmos para o primeiro gráfico, veremos que cada praia parece ter seu próprio intercepto e inclinação, o que torna plausível pensarmos que o modelo com a interação se ajuste melhor aos nosso dados.

Para modelos que podem ter mais de um efeito aleatório, Zuur et al. (2009), sugere um protocolo para a escolha da melhor estrutura de efeitos aleatórios. Vamos aos passos:

1. A primeira coisa a ser feita é ajustar um modelo com todos os efeitos fixos que estão sendo testados (modelo “completo”). No nosso exemplo tínhamos apenas NAP, mas vamos incluir Exposure (como fator fixo) para exemplificar melhor, e vamos incluir a interação entre NAP e Exposure. No nosso modelo “completo” a estrutura fixa é:

Richness ~ fExposure + NAP + fExposure:NAP + “efeito(s) aleatório(s)”

Podemos usar o símbolo (*) para simplificar a sintaxe, pois esse símbolo significa incluir o efeito sozinho e também suas interações. Escrevendo o mesmo modelo de forma simplificada (usando o asterisco):

Richness ~ fExposure * NAP + “efeito(s) aleatório(s)”

2. Depois que escolhemos o modelo “completo”, adicionamos os efeitos aleatórios plausíveis. No nosso exemplo, escolhemos duas possibilidades de efeito aleatório, variações no intercepto entre praias ((1|Beach)) e a interação entre praia e NAP, resultando também na variação de inclinação entre praias ((NAP|Beach)). Podemos também ajustar um modelo sem efeito aleatório (usando a função `lm`) e ver se a inclusão do efeito aleatório resulta num melhor ajuste do modelo:

# os modelos possíveis do nosso exemplo
m0 <- lm(Richness ~ fExposure * NAP, data = dados) #sem efeito aleat.
m1 <- lmer(Richness ~ fExposure * NAP + (1|Beach), data = dados)
m2 <- lmer(Richness ~ fExposure * NAP + (NAP|Beach), data = dados)

Um ponto importante é que estes modelos serão ajustados utilizando uma forma diferente de estimação, ao invés da máxima verossimilhança (ML), vamos usar a máxima verossimilhança restrita (REML). Isso acontece porque a ML é enviesado para as estimativas de variância do modelo e a REML corrige este enviesamento. Na prática, nós não precisamos fazer nada, pois a função `lmer` já usa, por padrão, a REML (argumento REML = TRUE).

3. Vamos utilizar o comando anova como temos feito para fazer a seleção dos modelos aninhados, buscando sempre a simplificação do modelo ao mínimo adequado. Aqui utilizamos o argumento refit = FALSE para garantir que a função irá manter a estimativa do REML.

anova(m1, m2, refit= FALSE)

Aqui o valor de p é alto indicando que os modelos não apresentam diferenças marcantes, sendo assim, devemos reter o modelo mais simple e seguimos simplificando.

anova(m1, m0, refit= FALSE)

Aqui, por outro lado, o valor do p é baixo e retemos o modelo mais complexo, ou seja aquele com o variável praia no efeito aleatório do intercepto.

Bom, agora sabemos que a melhor estrutura de efeito aleatório é apenas a variação no intercepto entre as praias. Assim, podemos prosseguir com a verificação dos efeitos fixos através de teste de hipóteses e/ou seleção de modelos.

Nessa parte, depois de já escolhermos a estrutura aleatória do nosso modelo, podemos averiguar qual a real influência dos efeitos fixos na riqueza de espécies, utilizando o procedimento que temos adotado nessa disciplina, o Teste de Hipóteses através da comparação de modelos pela tabela de ANOVA. E, depois de selecionado o modelo mínimo adequado, que melhor se ajusta aos dados, vamos fazer o diagnóstico dos resíduos deste modelo para ver se ele atende às premissas de um modelo linear misto.

Você pode perceber que o output da função `lmer` não dá as estatísticas t e o valor de P, dos parâmetros fixos do modelo como faz um `lm` (veja o summary do nosso primeiro modelo e compare com o `m0`). Isso porque a chamada “estatística Wald” não é recomendada para modelos mistos (sobre isso melhor olhar nas referências recomendadas). O que se faz para saber se uma variável é significativa ou não é construir modelos aninhados (ou seja, retirando um parâmetro do modelo com mais parâmetros) e comparando por uma tabela de Análise de Variância.

Nesse caso, precisamos ajustar nosso modelo por máxima verossimilhança (ML), pois é o indicado para compararmos modelos com diferentes efeitos fixos, mas com mesmo efeito aleatório. Então colocamos o argumento REML = FALSE no nosso modelo:

# modelo com interação entre Exposure e NAP
m1 <- lmer(Richness ~ fExposure + NAP + fExposure:NAP + (1|Beach), data = dados, REML = F)

# modelo sem interação entre exposure e NAP
m3 <- lmer(Richness ~ fExposure + NAP + (1|Beach), data = dados, REML = F)

E aplicamos a função anova nos nossos modelos aninhados:

anova(m1, m3)

Como o resultado da comparação entre os modelos foi significativo, nós retemos o modelo mais complexo, ou seja, o modelo com interação. O que podemos fazer é assegurar que o modelo com interação é também diferente do modelo nulo (sem efeitos fixos):

# modelo nulo

m6 <- lmer(Richness ~ 1 + (1|Beach), data = dados, REML = F)

anova(m1, m6)

Sim! Então podemos concluir que tanto `Exposure` quanto `NAP` influenciam na riqueza de espécies. Caso não tivesse havido diferença entre o modelo com interação e sem, nós deveríamos prosseguir com a seleção de modelos, fazendo a comparação entre o modelo com as duas variáveis e modelos com cada variável separadamente.

Vamos observar o resumo do nosso modelo selecionado:

summary(m1)

Depois de selecionado o modelo que melhor se ajusta aos nossos dados, vamos avaliar o ajuste deste modelo e suas premissas.

O primeiro diagnóstico do modelo é verificar se os resíduos são normalmente distribuídos, para isso geralmente usamos um qqplot (gráfico de quantil-quantil da distribuição normal) e possivelmente um teste de normalidade (por exemplo o Shapiro-Wilks). Além disso podemos também checar visualmente a homogeneidade de variância dos resíduos (homocedasticidade), ou seja, se a variablidade dos resíduos se mantém constante em relação aos valores ajustados.

Para isso usamos a função `plotresid` do pacote `RVAidememoire`:

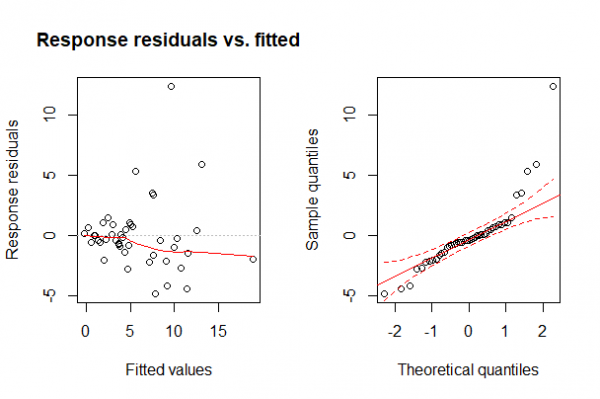
library(RVAideMemoire)

plotresid(m1, shapiro = T)

Se você se interessou pelos modelos mistos e acha que eles se encaixam no seu problema, não deixe de conferir as referências que a gente listou abaixo para se aprofundar nesse universo!!

lm(dependente ~ preditora, data = seus dados)