Antes de iniciar o roteiro, assista a aula gravada no nosso canal do Youtube.

O objetivo desse roteiro é auxiliar na compreensão de dois conceitos fundamentais do teste de hipótese estatística. O primeiro é entender o significado do p, ou a probabilidade de que, num cenário na qual a hipótese nula seja verdadeira, uma estatística de interesse tomada a partir de uma amostra seja igual ou mais extrema do que o valor observado. Dessa forma, o valor de p é um indicador da compatibilidade entre o conjunto de dados coletados e a hipótese nula. Suponha um valor de p muito pequeno (próximo de 0,001). Isso significa que é pouco provável que a diferença observada (estatística de interesse) tenha sido obtida caso a hipótese nula fosse verdadeira (alta incompatibilidade). Diante de um resultado pouco provável, rejeitamos a hipótese nula e ficamos com a hipótese alternativa que pressupõe algo mais, além da variação aleatória. Se por outro lado, o valor de p é próximo de 1,00, significa que a diferença observada tem alta probabilidade de ser gerada a partir do cenário nulo, ou seja, de que a diferença observada seja atribuída apenas à variação aleatória decorrente do acesso limitado aos dados (alta compatibilidade). Mas qual deve ser o ponto de corte, ou seja, a partir de que valor crítico de P devemos aceitar ou rejeitar a hipótese nula? Convencionou-se arbitrariamente, em muitas áreas da ciência, que tal valor crítico é de 0.05 ou 5%.

O segundo objetivo desse roteiro é definir quando devemos aplicar um teste unicaudal ou bicaudal e como isso se relaciona à nossa hipótese estatística e à nossa hipótese científica. É muito importante que, além de fazer o roteiro, você discuta com colegas e professores os conceitos apresentados.

Antes de iniciar o roteiro propriamente dito é necessário instalar os programas que iremos utilizar.

Para rodar esse roteiro utilizaremos duas ferramentas para o ensino de estatística desenvolvida por pessoas ligadas ao departamento de ecologia do IBUSP. O primeiro é o pacote Rsampling que contém instrumentação de permutação e aleatorização para a linguagem R. O outro é uma interface gráfica (Rsampling-shiny) para usar as ferramentas deste pacote no seu navegador. Não há necessidade de conhecimento prévio em R para fazer esse roteiro.

O primeiro passo é baixar a interface gráfica e descompactar o arquivo em um diretório conhecido no seu computador. Sugerimos que crie uma pasta para a disciplina “planeco” dentro da pasta de documentos do computador que está trabalhando.

Baixe, para essa pasta, o arquivo “source code” zip ou tar.gz¹⁾ da versão mais recente (1.7.0) do Rsampling-shiny no link:

• Versões Rsamping-shiny

Descompacte o arquivo na mesma pasta.

Depois de descompactar e testar o funcionamento (com os passos abaixo), você pode deletar o arquivo .zip ou .tar.gz

Abra o R pelo ícone do programa ²⁾ instalado em seu computador. Usando o menu Arquivo > mudar dir…. mude o diretório de trabalho para o diretório (i.e. a pasta) em que você salvou o Rsampling. Caso não tenha o R instalado no computador, veja algumas dicas de como instalar o R em nosso wiki.

Em seguida copie e cole a seguinte linha de comando no terminal do R para instalar os pacotes associados:

install.packages(c("Rsampling", "shiny", "PerformanceAnalytics"))

A seguinte mensagem irá aparecer no terminal do R “— Please select a CRAN mirror for use in this session —” e uma janela irá se abrir para que selecione o repositório mais próximo. Selecione Brazil(SP 1). Aguarde a instalação dos pacotes finalizar.

Agora digite as seguintes linhas de comando no terminal do R. A primeira linha irá ativar o pacote shiny que acabou de instalar, a segunda irá alterar o idioma para português e a terceira irá abrir a interface Rsampling-shiny no seu navegador, a partir do nome do diretório que descompactou. Sempre que quiser abrir a interface, deve digitar essas três linhas a partir do diretório da disciplina, não há necessidade de instalar os pacotes novamente ³⁾.

library(shiny)
language="pt"
runApp("Rsampling-shiny-1.7.0")

Se tudo correu bem, a seguinte interface deverá estar aberta no navegador:

A interface Rsampling tem 5 abas (em português: Rsampling, Tutorial, Entrada de dados, Estatística, Reamostragem). Explore as abas.

Nesta sessão vamos nos ater ao exemplo “Árvores de Mangue” baseado em um trabalho de alunos de pós-graduação durante o curso de campo em nosso programa. Abaixo a descrição da coleta dos dados⁴⁾.

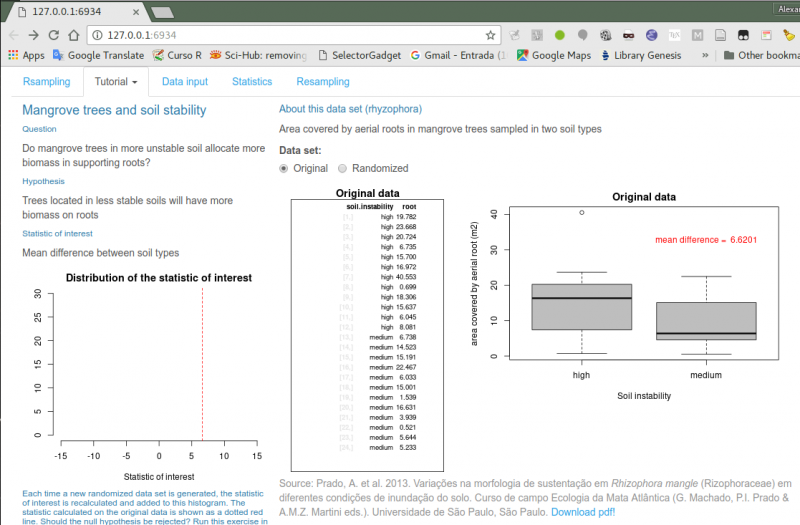
Abra o Rsampling-shiny e na aba tutorial o relacionado à árvores do mangue e estabilidade do solo.

Entender a hipótese e sua conexão com a estatística de interesse é crucial para compreender o que segue. Aqui estamos utilizando uma estatística de interesse bastante intuitiva, a diferença entre as médias de áreas de raizes dos diferentes solos. Faça uma breve pausa e reflita sobre como a diferença de área de raízes média entre os tipos de solo se conecta com a hipótese. Anote suas dúvidas para a discussão.

Iremos tratar a conexão entre estatística de interesse e hipótese em outros momentos durante o curso, mas não deixe que esses conceitos fiquem sem ser entendidos ao final deste módulo da disciplina.

Agora precisamos definir um cenário associado à hipótese nula, o nosso cenário nulo. Em geral, o cenário nulo está vinculado à explicação mais simples ou à ausência de efeitos relacionados à hipótese. No exemplo do mangue seria a ausência de efeito na área de raízes relacionada ao tipo de solo. Ou posto de outra forma, não há diferença detectável de área de raízes das árvores entre os tipos de solos.

Uma questão que emerge nesse ponto é: o que pode ser considerado ausência de efeito ou diferença detectável? Afinal, mesmo em um cenário nulo não esperamos que os valores das áreas de raizes sejam exatamente iguais, mesmo das árvores que estão em um mesmo tipo de solo.

É certo que existem outros fatores, além do tipo de solo, que podem influenciar o desenvolvimento das raízes de uma árvore. Por exemplo, a idade do indivíduo, variações de desempenho entre indivíduos de mesma idade e mesmo a variação associada ao processo de amostragem, isso só para citar algumas de muitos fontes possíveis. Portanto, precisamos diferenciar a variação associada a outros fontes, daquela que estamos interessados, no caso o solo. O que iremos fazer a seguir é simular cenários em que toda a variabilidade existente vem de outras fontes que não seja o solo. Como não sabemos exatamente quais são essa muitas outras fontes possíveis de variação e por gerarem variação imprevisível, vamos chamar essa variabilidade de aleatória.

Para gerar o cenário nulo podemos usar um procedimento simples que é desestruturar a fonte de variação de interesse. Ou seja, pegamos os valores de área de raízes e rearranjamos esses valores entre os tipos de solos de forma aleatória. Nesse momento, qualquer diferença que apareça nos dados é proveniente de outras fontes que não o tipo de solo.

Se repetirmos esse procedimento muitas vezes, quais valores da estatística de interesse seriam mais frequentes, partindo da premissa que nosso cenário nulo é verdadeiro?

Podemos responder essas questões utilizando a interface do RSampling, como segue abaixo.

Caso tenha entendido o procedimento que gera o cenário nulo por aleatorização, podemos partir para o teste de hipótese seguindo os passos definidos abaixo.

Uma decisão, tomada no começo do tutorial, não foi apresentada anteriormente: o teste feito até agora é unicaudal. O que significa isso? Mude a opção na aba de Reamostragem na barra Alternativa de “Maior que” para “Bicaudal”.

• Caso ainda não tenha feito, anote o seu nome, altura (em centímetros e sem decimais) e sexo (M, F) na planilha altura alunos.

• aguarde todos os alunos preencherem
• salve a planilha no seu computador, usando o formato .csv
• importe a planilha para o Rsampling, usando na aba “Entrada de Dados” a opção “Upload file”
• selecione a opção “Cabeçalho?”
• com esse conjunto de dados, teste as seguintes hipóteses usando o Rsampling:
  • altura média entre gêneros é diferente;
  • altura média de estudantes do sexo masculino é maior que de estudantes do sexo feminino.