Ferramentas do usuário
cursos:planeco:roteiro:07a-clasrcmdr
Gerenciador de mídias
Espaços de nomes
Selecione o espaço de nomes
Arquivos de mídia
Arquivos em cursos:planeco:roteiro

- adubo01.png
- 578×990
- 2020/03/11 16:21
- 132.4 KB
- adubo02.png
- 673×1001
- 2020/03/11 16:29
- 154.4 KB

- alfaceAleat.png
- 671×673
- 2024/02/29 18:25
- 65.6 KB
- alfaceDet.png
- 671×673
- 2024/02/29 18:25
- 41.2 KB

- alturaCresc.txt
- 2024/04/03 15:06
- 3.3 KB
- anova01.png
- 949×897
- 2020/04/22 09:30
- 148.4 KB
- anova01_nome_variavel_fExp_corrigido_dri.png
- 763×810
- 2020/04/25 19:55
- 210 KB
- autocorr.csv
- 2019/04/09 23:00
- 2.6 KB
- autocorr_2019_valores_positivos.csv
- 2019/04/09 22:30
- 2.6 KB
- birds_clim.csv
- 2020/04/11 18:10
- 9.5 KB
- bivar.csv
- 2019/04/09 23:00
- 1.4 KB

- boxplotAnova.png
- 524×524
- 2022/03/25 10:25
- 23.2 KB

- cegonha final_133910457_dreamstime.jpg
- 241×220
- 2020/04/12 15:45
- 13.5 KB
- centerAgeBabies.png
- 731×517
- 2022/04/13 16:20
- 53.4 KB
- compareAnovaLag00.png
- 829×492
- 2022/04/02 12:17
- 48.2 KB
- corPeso.png
- 930×477
- 2024/03/23 13:46
- 60.5 KB

- crawley.png
- 134×186
- 2019/03/29 09:59
- 37 KB

- crescArv.txt
- 2024/04/04 15:14
- 3.3 KB
- crop.png
- 1076×761
- 2019/03/29 10:00
- 93.1 KB

- crop.xlsx
- 2019/03/29 09:58
- 5.8 KB

- crop1aAnova.xlsx
- 2020/03/12 10:19
- 6.5 KB

- crop1Anova.xlsx
- 2020/03/12 10:21
- 5.3 KB
- crop2Anova.csv
- 2019/04/09 11:19
- 544 B
- crop2nova.png
- 685×1007
- 2019/04/09 11:20
- 130.2 KB

- crop2novaFim.png
- 519×926
- 2019/04/09 15:16
- 111.3 KB

- cropMult.xlsx
- 2020/03/12 11:56
- 5.3 KB
- cropMult01.jpg
- 554×878
- 2020/03/12 11:57
- 139.7 KB
- cropMult02.jpg
- 572×883
- 2020/03/12 12:16
- 164.3 KB

- datamodel.jpg
- 930×624
- 2020/03/12 10:12
- 179.8 KB

- diagnostico_chuva.png
- 1784×1652
- 2022/03/23 16:00
- 784.8 KB

- digPraia.png
- 523×524
- 2020/04/26 14:06
- 17.1 KB
- equacaoXYmod1.png
- 763×620
- 2019/04/10 10:30
- 218.8 KB
- figura2_aves_mundo_triantis_matthews2020_nature.jpg
- 354×197
- 2020/04/12 16:07
- 25.7 KB

- figura2_aves_mundo_triantis_matthews2020_nature.png
- 716×484
- 2020/04/12 16:15
- 186.2 KB

- Figura matriz correlacao.jpg
- 284×265
- 2020/04/12 15:49
- 32.7 KB

- Figura matriz correlacao.png
- 750×750
- 2020/04/12 15:41
- 18.4 KB

- Figura Split Plot oats.png
- 720×540
- 2020/04/26 02:18
- 47.4 KB

- FiguraGotelli.png
- 1000×1135
- 2020/03/12 12:21
- 324.3 KB

- FiguraGotelli_corrigida.pdf
- 2020/04/08 10:46
- 285.3 KB

- FiguraGotelli_corrigida.png
- 1055×1162
- 2020/04/09 18:11
- 346.7 KB
- final_aed.csv
- 2019/04/08 16:59
- 1.5 KB

- Fisher_et_al-2018-Ecology_and_Evolution.pdf
- 2019/04/09 17:07
- 604.4 KB

- FloradaIpesPantanal.png
- 1500×998
- 2019/04/22 13:57
- 2.4 MB
- fluxo_ppt.csv
- 2019/04/07 20:57
- 1.8 KB
- graficoBoxPlots.png
- 982×814
- 2019/04/14 09:42
- 215.9 KB
- instalpkg.png
- 714×720
- 2019/04/14 09:26
- 94.9 KB

- lagarta.txt
- 2022/04/01 17:54
- 63 B

- lagartaColors.jpg
- 265×190
- 2019/04/01 15:31
- 12.9 KB

- lagartaTrans.png
- 265×190
- 2019/04/01 15:37
- 111.7 KB

- lmComics.jpg
- 478×232
- 2019/04/01 15:49
- 32.6 KB

- lmComicsTrans.jpg
- 477×233
- 2019/04/01 15:47
- 41.9 KB

- lmComicsTrans.png
- 478×232
- 2019/04/01 15:49
- 107.7 KB
- lmCreateDesvios.png
- 773×660
- 2022/03/29 17:13
- 67.8 KB

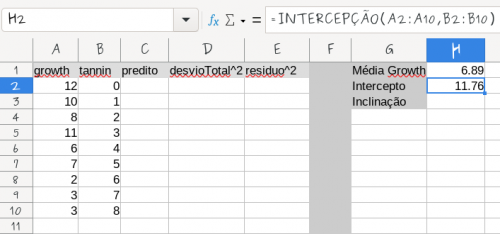
- lmExcel01.png
- 707×332
- 2022/04/01 11:56
- 28.4 KB
- lmLag.png
- 721×661
- 2022/04/01 18:04
- 61.9 KB
- lmLag00.png
- 682×666
- 2022/04/01 18:18
- 61 KB
- lmmanova00.png
- 750×384
- 2020/04/22 09:24
- 72.6 KB
- lmmanova02.png
- 915×717
- 2020/04/22 10:27
- 115.3 KB
- lmmfull.png
- 803×786
- 2020/04/22 09:15
- 141.2 KB
- lmmint.png
- 817×816
- 2020/04/22 09:18
- 144.9 KB

- LMMModel.png
- 523×524
- 2019/04/29 16:45
- 56.3 KB
- lmmriq.png
- 625×611
- 2020/04/22 06:24
- 91.3 KB
- lmmriqCoefs.png
- 951×952
- 2020/04/22 07:31
- 146.3 KB

- lmmriqSummary.png
- 443×530
- 2020/04/22 06:28
- 46.7 KB
- loadMass.png
- 577×475
- 2020/04/24 07:54
- 83.2 KB
- loadPluginRcmdr.png
- 736×452
- 2019/04/14 09:32
- 66.8 KB

- MaguezalMarajo2.jpg
- 563×283
- 2022/04/15 14:19
- 67.2 KB
- mangrove.csv
- 2022/04/15 14:24
- 2.5 KB

- mangue.jpg
- 267×189
- 2022/03/21 16:34
- 13.9 KB

- manguezalMarajo.jpeg
- 563×283
- 2022/04/15 14:18
- 67.2 KB
- newVarFlower.png
- 693×415
- 2019/04/14 10:58
- 70.3 KB
- oatsData.png
- 549×457
- 2020/04/24 07:59
- 72 KB

- oatsHelp.png
- 1216×901
- 2020/04/24 09:28
- 97.1 KB
- oatsP.png
- 617×536
- 2020/04/24 10:29
- 79.7 KB
- oatsPlot.png
- 848×472
- 2020/04/26 08:32
- 109 KB

- percentis_normal_padronizada.jpg
- 960×720
- 2019/04/07 22:48
- 92.4 KB
- plankivore.csv
- 2019/04/09 17:02
- 2.1 KB
- plotBabies01.png
- 609×570
- 2022/04/14 13:32
- 78.8 KB
- plotpraia.png
- 899×951
- 2020/04/22 07:41
- 112 KB

- praia.txt
- 2020/04/26 07:42
- 1.2 KB

- praia01.txt
- 2020/04/26 07:43
- 1.2 KB

- praiasLMM.png
- 523×524
- 2020/04/22 08:04
- 50.1 KB

- produtividade_chuva.txt
- 2022/03/23 11:32
- 394 B

- produtividade_temp.txt
- 2022/03/23 16:43
- 340 B
- qqlot_fluxo_nascentes_exemplo.png
- 1004×1004
- 2019/04/07 23:29
- 77.4 KB
- quineGLM.png
- 703×664
- 2019/04/13 11:24
- 90.3 KB

- randfixEff.png
- 1050×254
- 2024/04/02 18:06
- 131.7 KB
- readLagarta.png
- 667×702
- 2022/04/01 17:56
- 56.1 KB
- readPraia.png
- 765×822
- 2020/04/22 06:06
- 107.3 KB
- resPeso.png
- 927×561
- 2024/03/23 13:29
- 70.6 KB

- richData.png
- 696×705
- 2019/04/29 14:29
- 26.5 KB

- richGLMM.png
- 523×524
- 2019/04/29 16:02
- 69 KB

- richModel.png
- 523×524
- 2019/04/29 14:59
- 56.3 KB

- solosAnova.png
- 756×573
- 2020/03/02 15:34
- 33.2 KB

- species.txt
- 2019/04/09 20:12
- 1.8 KB
- speciesLMres.png
- 1326×890
- 2019/04/13 12:25
- 183.7 KB
- speciesPlot.png
- 1272×756
- 2019/04/13 12:06
- 147.9 KB

- statisticCartoon.png
- 719×292
- 2019/04/01 12:29
- 35.3 KB

- summary_model_chuva.png
- 1086×542
- 2022/03/23 15:40
- 84.1 KB
- summaryMod1xy.png
- 681×617
- 2019/04/10 10:32
- 192.8 KB
- summLmmint.png
- 715×753
- 2020/04/24 09:08
- 100.6 KB

- tabTestes.png
- 1001×532
- 2019/03/29 09:46
- 53.1 KB
- testePPTanova01.png
- 763×810
- 2020/04/25 19:52
- 210 KB
- univar.csv
- 2019/04/09 22:59
- 7.9 KB
- univar1.csv
- 2019/04/07 20:56
- 7.9 KB

- varEntreAnova.png
- 769×580
- 2020/03/02 16:13
- 48.6 KB

- variacaoTotalAnova.png
- 771×575
- 2020/03/02 15:46
- 41.6 KB

- varIntraAnova.png
- 765×585
- 2020/03/02 16:02
- 40.6 KB
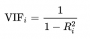
- VIF_equation.png
- 280×122
- 2020/04/17 16:06
- 1.6 KB
Arquivo
- Ver
- Histórico
- Data:
- 2022/04/01 11:56
- Nome do arquivo:
- lmexcel01.png
- Formato:
- PNG
- Tamanho:
- 28KB
- Largura:
- 707
- Altura:
- 332
- Referências para:
- Modelos Lineares I - Base
- Modelos Lineares Simples II
cursos/planeco/roteiro/07a-clasrcmdr.txt · Última modificação: 2024/03/08 13:01 (edição externa)
Exceto onde for informado ao contrário, o conteúdo neste wiki está sob a seguinte licença: CC Attribution-Noncommercial-Share Alike 4.0 International