Ferramentas do usuário
Barra lateral
Tabela de conteúdos
Modelos Lineares
Os modelos lineares são uma generalização dos testes de hipótese clássicos mais simples. Uma regressão linear, por exemplo, só pode ser aplicada para dados em que tanto a variável preditora quanto a resposta são contínuas, enquanto uma análise de variância é utilizada quando a variável preditora é categórica. Os modelos lineares não têm essa limitação, podemos usar variáveis contínuas ou categóricas indistintamente.
ERRATA: por volta de 16'28“ digo que o valor da inclinação na população é 3,5 quando o correto é 2,5
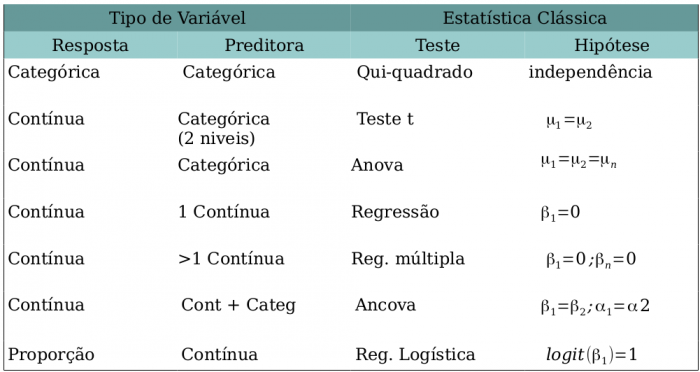
No nosso quadro de testes clássicos frequentistas, definimos os testes baseados na natureza das variáveis respostas e preditoras.
Os modelos lineares dão conta de todos os testes apresentados na tabela acima que tenham a variável resposta contínua. Portanto, já não há mais necessidade de decorar os nomes: teste-t, Anova, Anova Fatorial, Regressão Simples, Regressão Múltipla, Ancova entre muitos outros nomes de testes que foram incorporados nos modelos lineares. Isso não livra o bom usuário de estatística de entender a natureza das variáveis que está utilizando. Isso continua sendo imprescindível para tomar boas decisões ao longo do processo de análise e interpretação dos dados.
Simulando Dados
Modelos Lineares
Os modelos lineares são uma generalização dos testes de hipótese clássicos mais simples. Uma regressão linear, por exemplo, só pode ser aplicada para dados em que tanto a variável preditora quanto a resposta são contínuas, enquanto uma análise de variância é utilizada quando a variável preditora é categórica. Os modelos lineares não têm essa limitação, podemos usar variáveis contínuas ou categóricas indistintamente.
ERRATA: por volta de 16'28“ digo que o valor da inclinação na população é 3,5 quando o correto é 2,5
No nosso quadro de testes clássicos frequentistas, definimos os testes baseados na natureza das variáveis respostas e preditoras.
Os modelos lineares dão conta de todos os testes apresentados na tabela acima que tenham a variável resposta contínua. Portanto, já não há mais necessidade de decorar os nomes: teste-t, Anova, Anova Fatorial, Regressão Simples, Regressão Múltipla, Ancova entre muitos outros nomes de testes que foram incorporados nos modelos lineares. Isso não livra o bom usuário de estatística de entender a natureza das variáveis que está utilizando. Isso continua sendo imprescindível para tomar boas decisões ao longo do processo de análise e interpretação dos dados.
Simulando dados - Modelo I
Vamos começar com um exemplo simples de regressão, mas de forma diferente da usual. Vamos usar a engenharia reversa para entender bem o que os modelos estatísticos estão nos dizendo e como interpretar os resultados produzidos. Podemos, por exemplo, começar simular o que supostamente encontramos na natureza e produzir eventos de coletas de dados, com a estrutura muito similar ao que supostamente encontramos na realidade. Depois disso, usamos esses dados simulados para entender o que os modelos nos transmitem de informação, baseado em uma população estatística que conhecemos as características. Normalmente o que fazemos no procedimento científico é o inverso, tomamos uma amostra de uma população estatística no sistema de interesse e, a partir dela tentamos inferir os processos que estão agindo no sistema todo.
A primeira parte é estabelecer qual o modelo matemático que descreve o processo que estamos interessados. Esse modelo, neste caso, tem dois componentes principais acopladas: (1) uma estrutura determinística e outra aleatória. A primeira está relacionada ao processo de interesse e relaciona a variável resposta à preditora. Pensando em um caso mais simples, essa estrutura é um modelo matemático linear e tem a seguinte forma:
$$ y = {\alpha} + {\beta} x$$
Note que estamos usando uma notação diferente da aula de regressão linear, mas a expressão é a mesma:
$\alpha$ = A
$\beta$ = B
Ou seja, os parâmetros da população ao qual não temos acesso que definem (1) o valor da variável resposta quando a preditora é zero (intercepto) e (2) o quanto a resposta varia quando aumentamos uma unidade na preditora (inclinação).
O componente aleatório, ou a variabilidade do modelo, é expresso por uma variável probabilística Gaussiana da seguinte forma:
$$ \epsilon = N(0, \sigma) $$
Portanto, nossos dados serão uma amostra de uma população com a seguinte estrutura:
$$ y = {\alpha} + {\beta} x + \epsilon$$
Para tornar essa abstração um pouco mais conectada com a realidade vamos imaginar um experimento do efeito de adubo orgânico em canteiros de hortaliças (alface, por exemplo). O adubo orgânico é medido em massa (kg/m²) e a podução de alface medida em quilogramas por canteiro. Nesse experimento hipotético, queremos saber, primeiro se o adubo afeta a produtividade do alface e segundo, se afeta, qual é o tamanho deste efeito. Nossa variável resposta y neste caso seria a produtividade do alface ($kg/m^2$), nossa variável preditora x é a quantidade de adubo colocado nos canteiros. O que buscamos estimar é o $\beta$ (inclinação) ou seja, quanto a produtividade do alface aumenta com o aumento de 1 unidade (kg) de adubo. Esse é o efeito que estamos interessados. Neste caso, o $\alpha (intercepto) é o quanto temos de produtividade de alface quando colocamos zero unidades de adubo orgânico no canteiro, ou seja o crescimento do alface sem adubação.
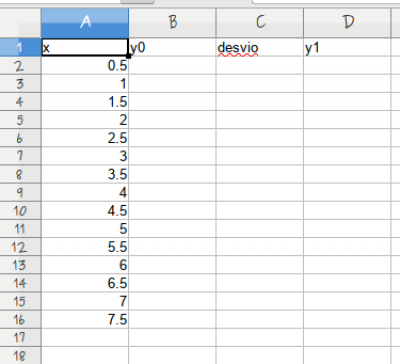
Parece complicado, mas é razoavelmente simples gerar dados em nosso computador com a estrutura matemática acima. Primeiro vamos criar a variável x que é o quanto de adubo é colocado nos canteiros de alface. No nosso desenho experimental definimos previamente colocar no mínimo 0,5 kg/m² e no máximo 7,5 kg/m² de adubo nos canteiros, em intervalos de 0,5 kg/m², totalizando 15 canteiros. Além disso, distribuímos esses canteiros de forma aleatória em nosso sítio, todos no mesmo tipo de solo1).
- nomeie a coluna A como
adubo(kg/m²)na célula A1; - preencha as células
A2:A16com uma sequência de valores de 0.5 a 7.5, em intervalos de 0.5
Em seguida vamos estabelecer a estrutura determinística que define a relação entre x e y. Para tanto precisamos definir dois valores: (1) qual o crescimento do alface quando não colocamos adubo, o intercepto do modelo e (2) quanto o adubo afeta o crescimento do alface, a inclinação do modelo. Nessa primeira simulação da população, vamos definir o crescimento do alface sem adição de adubo como sendo 4 kg por canteiro e o incremento na produtividade do alface ao acrescentar 1 kg/m² de adubo como sendo 3,5 kg, respectivamente nosso intercepto e inclinação. Nesse sistema simulado sabemos que os canteiros sem adubo, em média, produzem 4 kg de alface e que o efeito de adicionar 1 kg/m² de adubo no canteiro aumenta a produtividade em 3,5 kg. Também definimos que este aumento é constante, ao menos no intervalo de valores de adubo do experimento2). Ou seja, um canteiro onde foi adicionado 1 kg/m² de adubo produz, em média 7,5 kg de alface e no que foi adicionado 2 kg/m² produz 11 kg de alface.
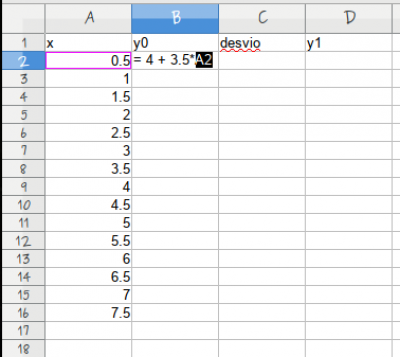
- nomeie a coluna B como média de produção (kg) na célula B1;
- preencha a célula B2 com a fórmula = 4 + 3.5 * A2
- copie a formula para as células B3:B16, clicando e arrastando o mouse quando aparecer no canto inferior esquerdo da célula B2 o sinal de
+. - construa o gráfico de dispersão com essas duas colunas, sendo adubo a variável preditora no eixo
xe a produção de alface como resposta no eixoy
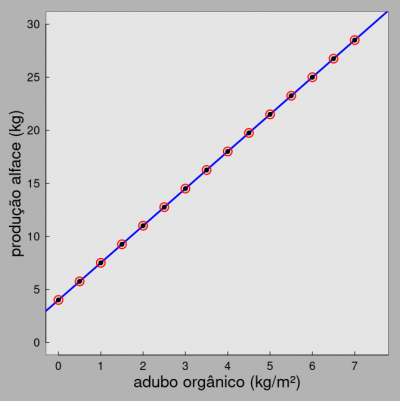
Neste momento, temos a estrutura determinística do modelo representada no gráfico abaixo:
Essa representação não parece muito realista. Ela define a relação entre adubação e a produtividade de alface como sendo absolutamente perfeita! Chamamos esses valores de esperança ou predição do modelo. Sabemos que existem muitos outros fatores que podem afetar a produtividade do cultivo do alface além da adubação. Mesmo que o desenho experimental tenha controlado todos os outros fatores de confusão importantes, haverá algum grau de variação na produtividade do alface não relacionada à adubação. Por exemplo, apesar de termos colocado os tratamentos (canteiros) em mesmo tipo de solo, a condição de umidade pode variar pela proximidade com pequenos riachos ou por variações na microtopografia. A quantidade e qualidade da luz que incide sobre os canteiros pode variar dependendo do entorno do canteiro e da declividade do terreno. Além desse efeitos externos, mesmo que as sementes venham de um mesmo fornecedor, pode haver pequenas variações genéticas entre elas que definem variação na produtividade potencial. Todos essas possíveis fontes de variação, mesmo que pequenas, geram variação na produtividade dos canteiros
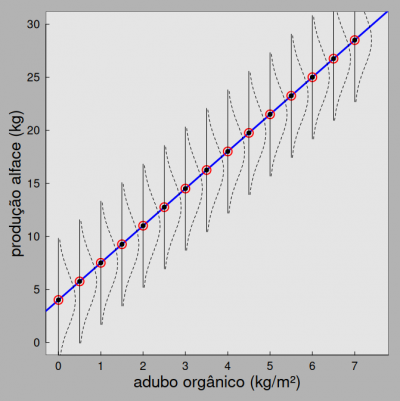
A estrutura aleatória em nosso modelo irá gerar essa variabilidade estocástica do sistema, ou seja, ela está relacionada a todos os outros fatores não contemplados em nosso desenho experimental que geram variação na produtividade do alface. No caso, uma estrutura de distribuição aleatória normal com média 0 e desvio padrão 7. O gráfico a seguir representa essa estrutura estocástica na estrutura determinístico do modelo.
As representações das curvas em forma de sino deitado representam a probabilidade de um canteiro, em cada nível de adubação, desviar do valor definido pela esperança do modelo. A probabilidade de um canteiro qualquer apresentar produtividade maior ou menor do que o predito pelo modelo, diminue conforme se afastam dessa predição média do modelo. Vamos gerar então uma realização aleatória de produtividade no canteiro à partir de cada uma dessas curvas.
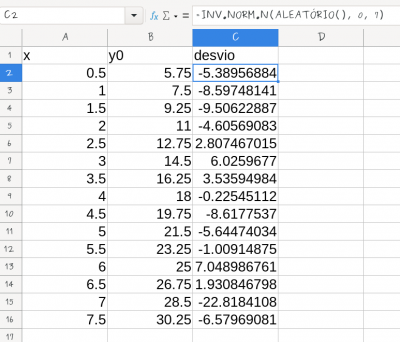
- nomeie a coluna C como desvio na célula C1;
- preencha a célula C2 com a fórmula
= INV.NORM.N(ALEATÓRIO(); 0 ; 7)3). Essa fórmula vai retornar valores aleatórios tomados de uma distribuição normal com média 0 e desvio padrão 7; - copie a formula para as células C3:C16, clicando e arrastando o mouse quando aparecer no canto inferior esquerdo da célula B2 o sinal de
+.
A função INV.NORM.N() tem três parâmetros, (1) probabilidade, (2) média e (3) desvios padrão. O primeiro valor define a probabilidade cumulativa da distribuição normal que iremos sortear ao incluirmos a função ALEATÓRIO() colocamos um valor aleatório entre 0 e 1. A média e o desvio padrão são os parâmetros que definem a função probabilística normal. A média é zero pois iremos somar o predito pelo modelo em seguida. O desvio padrão define o quanto o formato do sino é mais adensado ou disperso ao redor da média.
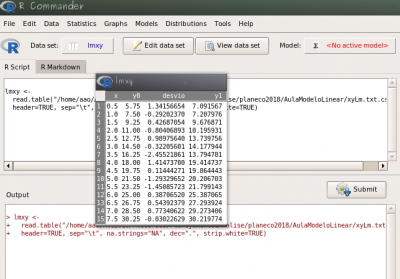
- nomeie a coluna D como produção de alface (kg) na célula
D1; - A variável y1 na coluna D é a soma do valor da coluna B com o valor da coluna C (
y0+ desvio). Para fazer isso, coloque na célula D2 a função=soma(B2:C2)ou=B2+C2, depois copie para as outras células da coluna; - salve a planilha como texto separado por vírgulas e use o nome xy.csv
Note que a cada vez que faz algum cálculo na planilha os valores dos desvios são atualizados, ou seja, uma nova realização da amostra de canteiros é feitas da pela função INV.NORM.N e os valores da coluna desvios atualizados. Para evitar esse comportamento podemos selecionar os valores desta coluna e usar Editar > Colar especial e usar a opção de colar apenas os valores numéricos, com isso a formula some e os valores não são mais atualizados a todo momento.
Modelo Linear Simples
Vamos agora usar esse dados para estudar o modelo linear e entender as informações que são fornecidas por ele.
Estimando parâmetros: Modelo I
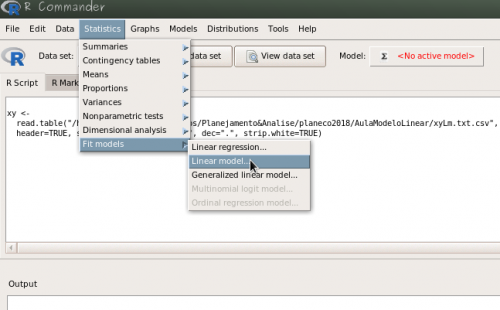
Use a interface do Rcommander para construir o modelo linear e estimar os parâmetros:
- Defina o nome desse modelo como mod1
- A fórmula do modelo tem duas caixas. Na caixa da esquerda (antes do símbolo
~) você deve colocar a variável respostay, que nesse caso é a nossa variávelprodução de alface (kg). - Na caixa da direita (após o
~) coloque a variável preditorax, que nesse caso é a variáveladubo(kg/m²)
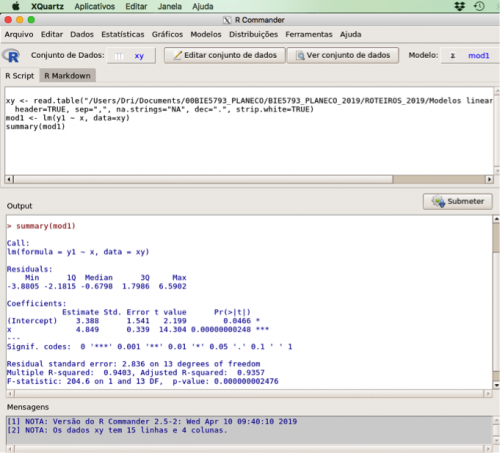
- interprete o resultado do ajuste. Onde está o valor da inclinação da reta ajustada?
- copie o resultado do summary do modelo que aparece na janela Output4)
Resultados do Modelo I
Anote os valores do resultado da análise na planilha modelo linear I que estamos preenchendo para todos as versões do curso, coloque seus dados ao final das linhas preenchidas e na coluna ano, coloque o ano em que cursou PlAnEco.
ATENÇÃO: a planilha do google pode ter a decimal definida como ,! Confira ao fazer a transposição dos valores, garanta que a planilha está lendo os valores como numéricos.
Múltiplos Experimentos - Modelo I
A estatística frequentista define que uma amostra e seus resultados são apenas uma realização dentre as possíveis provenientes de uma população de amostras ao qual não temos acesso. Utilizando os resultados de outros alunos na tabela modelo linear I podemos simular essa múltipla realizações de experimentos e investigar alguns conceitos importantes.
- Baixe a planilha modelo linear I no seu computador, depois de incluir o seu dado. Não se preocupe em esperar todos os colegas completarem a planilha, repetimos algumas vezes a simulação de dados para que possam usar, mesmo que nenhum outro aluno tenha feito ainda, Além disso, usamos os dados de alunos que cursaram PlAnEco em outros anos.
- Calcule a média e o desvio padrão dos parâmetros dessa planilha Não calcule nenhum valor diretamente na planilha do Google
- Calcule a proporção de vezes que o p-valor foi significativo.
Modelo II
Variabilidades e Incertezas
Vamos fazer uma pequena modificação na geração de dados simulados para entendermos como a variabilidade do sistema afeta a precisão das nossas estimativas. Para isso precisamos apenas mudar o parâmetro a variabilidade da nossa população: o desvio padrão da estrutura aleatória do modelo. Estamos fazendo com que as curvas em forma de sino do gráfico que exemplifica a estrutura aleatória do modelo fiquem mais abertos. Desta forma a probabilidade de amostrar valores mais distantes do predito pelo modelo aumenta e com isso a nossa população estatística incorpora maior variabilidade. Isso, por consequência, afeta nossas estimativas de parâmetros e sua precisão. Note que, a estrutura determinística do nosso modelo matemático permanece a mesma, ou seja, o efeito que a variável preditora x tem na variável resposta y permanece o mesmo. Além disso, nosso esforço amostral não foi alterado, apenas a variabilidade do sistema. Vamos investigar então o que acontece com nossas estimativas:
- simule um novo conjunto de dados usando os mesmo passos anteriores, mudando apenas o comando:
INV.NORM.N(ALEATÓRIO(); 0 ; 7)
para:
INV.NORM.N(ALEATÓRIO(); 0 ; 14)
- Salve o arquivo com os dado simulados pois iremos utilizá-lo no próximo roteiro;
- suba os dados para o Rcommander;
- construa o modelo no Rcommander;
- salve os resultados do modelo.
Resultado do Modelo II
- anote os resultados base do modelo na planilha modelo linear simples II
- depois de anotar seus resultados baixe a planilha no seu computador;
- faça os cálculos de médias e desvios padrão para os parâmetros de intercepto e inclinação desta planilha;
- compare os valores calculados acima com os do modelo anterior;
- verifique se os valores de desvio padrão da distribuição de intercepto e inclinação tem alguma conexão com os valores apresentados no resumo do modelo.
Modelo III
Esforço Amostral
Uma outra fonte de imprecisão nas estimativas do nosso modelo tem relação com o próprio desenho experimental e está associada ao tamanho da nossa amostra. Essa fonte de imprecisão, apesar de acoplada à variabilidade do sistema, pode ser minimizada com o aumento do esforço amostral. Vamos simular uma amostra maior para os dados simulados do Modelo II onde o desvio padrão da população é 14. Para aumentar o esforço amostral vamos modificar a sequência de valores de x na amplitude de 0,5 a 7,5 para intervalos de 0,14, totalizando 51 observações na nossa amostra.
Note que nessa nova simulação de dados não há nenhuma modificação do nosso sistema ou do modelo matemático subjacente. Todos os parâmetros da população e sua variabilidade intrínseca permanecem os mesmos da segunda simulação de dados (Modelo II). A única modificação é no desenho experimental onde o esforço amostral foi aumentado.
Para agilizar a construção desta sequência podemos criar um valor de referência para as observações de 0 a 50 e operar esse valor de referência.
- na célula A2 inicie em
0e crie uma sequencia de inteiros até50(célula A51), nomei essa coluna deseq; - na célula B2 coloque a fórmula
=0.5+(0.14*A2)e copie a fórmula para todas a coluna até a célula B51 isso irá criar nossa nova variávelx; - na coluna C crie a variável
y1com a mesma formula do modelo anterior= 4 + 3.5 * B2; - a partir deste ponto é só seguir os passos da simulação anterior notando que a variável
y1agora está na colunaC; - garanta que calculou os desvios com
INV.NORM.N(ALEATÓRIO(); 0 ; 14), como no exemplo anterior; - salve os dados simulados em um arquivo para uso posterior;
- crie o modelo no Rcommander;
- salve o resultado do modelo;
- anote os resultados do modelo gerado na planilha modelo linear III ;
- salve a planilha no seu computador;
- calcule a média e o desvio padrão para os parâmetros de intercepto e inclinação;
- compare esses valores com os valores calculados para o Modelo I.
Variáveis Indicadoras (Dummies)
No inicio deste tutorial dissemos que os modelos lineares unificaram muitos dos testes clássicos da estatística frequentista.
Uma dos elementos importantes para essa unificação foi a transformação das variáveis preditoras categóricas em variáveis indicadoras, também chamadas de dummies. O procedimento consiste basicamente em criar novas variável para representar as categoria da variável preditora. Para cada categoria há uma indicadora contendo 1 quando a observação pertence ao nível referente e 0 quando não pertence. Para cada nível precisamos de uma indicadora, com exceção do nível que é considerado basal, indicado pelo 0 em todas as outras variáveis indicadoras relativas aos outros níveis da variável categórica. Dessa forma, para uma variável preditora categórica com 4 níveis teremos 3 variáveis indicadoras no modelo e se tivermos duas variáveis categóricas preditoras, cada uma com 3 níveis, teremos 4 variáveis indicadoras, duas para cada variável.
No nosso exemplo de anova a variável preditora solo tinha os níveis: arenoso, argiloso e húmico.Neste caso, cada nível de solo seria representada pelas indicadoras da seguinte forma:
| variável indicadoras: | ||
| nível: | indica arenoso | indica húmico |
|---|---|---|
| arenoso | 0 | 0 |
| argiloso | 1 | 0 |
| húmico | 0 | 1 |
O resultado deste modelo irá apresentar um intercepto e dois coeficientes, um associado ao nível argiloso, outro ao nível humico. O nível arenoso, não contemplado com uma variável indicadora 7) é estimado no intercepto. Essa estimativa do intercepto, no caso do exemplo apresentado na aula de anova, representa a produção média nesse tipo de solo. Os outros coeficientes apresentados pelo modelo representam o quanto os solos argiloso ou humico são em média diferentes do arenoso. Vamos criar um modelo e interpretar os coeficientes em um conjunto de dados que tem a variável solo agora com quatro níveis.
- baixe o arquivo colheita.csv;
- abra no excel;
- note que a variável
solotem agora 4 níveis:arenoso,argiloso,humicoealagado; - calcule a média de produtividade para cada tipo de
solo; - Importe o arquivo original
colheita.csvpara o Rcommander; - Ajuste um modelo denominado de
lmSolono menuEstatística>Ajuste de Modelos>Modelo Linear. O modelo deve ser definido como na fórmula abaixo:
colhe~solo
- compare os coeficientes estimados pelo modelo com os valores de produtividade média para cada tipo de solo.
Para entender o procedimento das variáveis indicadoras vamos construir explicitamente nossas variáveis indicadoras.
- abra o arquivo colheita.csv no excel;
- crie 3 novas colunas nomeadas de:
arenoso,argiloso,humico. - para cada observação (linha) represente o nível do solo com o valor
1na respectiva indicadora e0nas outras. Note que um nível não precisa de indicadora pois será representado pela indicação de0em todas as indicadoras, no nosso caso o nívelalagado8); - salve a planilha no formato
.csv; - importe essa planilha com as variáveis indicadoras para o Rcommander;
- ajuste um modelo denominado de
lmSoloIndicacom as variáveis indicadoras no menuEstatística>Ajuste de Modelos>Modelo Linear. O modelo deve ser definido como na fórmula abaixo:
colhe ~ arenoso + argiloso + humico
- Para olhar a tabela de partição de variância, vá ao menu
Modelos>Testes de hipóteses>Tabela de ANOVA
- Compare os dois modelos
lmSoloelmSoloIndica
A transformação de variáveis resposta categóricas para variáveis indicadoras permite que o modelo linear possa tratar indistintamente variáveis categóricas e contínuas. Essa unificação simplifica muito a construção de modelos e sua operacionalização, entretanto, entender que as categorias foram transformadas em indicadoras é essencial para entender e interpretar o resultado apresentado pelos modelos lineares.
PARA ENTREGAR ANTES DO INÍCIO DA PRÓXIMA AULA
Preencha as perguntas no formulário abaixo até antes da próxima aula ou a data estipulada pela equipe da disciplina. Caso tenha algum problema, faça por esse link. Em caso de mais de uma submissão, a última, antes do final do prazo, será considerada.
Exercício Modelo Linear Simples
Responda o formulário abaixo.
Para enviar as respostas é necessário estar logado no wiki.
Utilize:
- usuário: alunos
- senha: planeco2020
Modelo Linear: partição da variação
Os modelos lineares podem ser analisados através do método de partição de variância que aprendemos no roteiro de Princípios da Estatística Frequentista. Caso não tenha sedimentado bem o conceito, retorne ao roteiro e reveja a videaula, isso será importante para acompanhar o restante deste roteiro. Assim como na análise de variância clássica onde a preditora é uma variável categórica, podemos particionar a variação total existente nos dados nas porções explicadas e não explicadas por uma variável contínua preditora. Esse particionamento da variação no caso de um modelo linear simples é análogo ao que acontece em uma análise de variância tradicional, com a diferença que essa última só pode ser aplicada para variáveis preditoras categóricas.
 A nossa próxima atividade usa os dados de crescimento de lagartas submetidas a dietas de folhas com diferentes concentrações de taninos presente no livro The R Book (Crawley, 2012). São apenas duas variáveis, growth, o crescimento da lagarta, e tannins, a concentração de taninos. O objetivo é verificar se há relação entre o crescimento da lagarta e a concentração de taninos da dieta.
A nossa próxima atividade usa os dados de crescimento de lagartas submetidas a dietas de folhas com diferentes concentrações de taninos presente no livro The R Book (Crawley, 2012). São apenas duas variáveis, growth, o crescimento da lagarta, e tannins, a concentração de taninos. O objetivo é verificar se há relação entre o crescimento da lagarta e a concentração de taninos da dieta.
Desvios Quadráticos
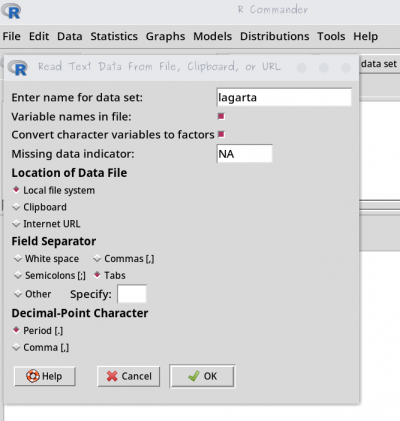
- baixe o arquivo regression.txt;
- abra o arquivo no Excel, selecionando a separação de campo como tabulação;
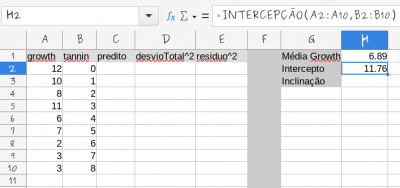
- calcule a média de crescimento das lagartas;
- calcule o intercepto e a inclinação do modelo linear no próprio excel, usando as funções descritas no quadro abaixo;
Para o cálculo dos parâmetros da reta use as funções do Excel:
- em uma coluna chamada desvio total calcule o desvio total de cada observação (o crescimento observado menos a média do crescimento);
- nomei uma coluna desvios quadráticos totais e eleve ao quadrado os valores da coluna criada anteriormente;
- some esses valores para obter a soma dos desvios quadráticos total nomeado como Variação Total
- calcule o valor predito pelo modelo em uma coluna chamada predito;
Predito pelo modelo
A predição do modelo é calculada pela equação da reta:
$$ \hat{y_i} = a + b * x_i $$
a = intercepto
b = inclinação
$x_i$ = valor de x da observação i
$\hat{y_i}$ = valor predito para a observação i
- em uma coluna chamada residuo calcule a diferença entre cada observação e o respectivo valor predito pelo modelo;
- crie uma outra coluna (residuo^2) com os valores de resíduos quadrático do modelo para cada observação (observado menos o predito pelo modelo ao quadrado);
- some os desvios quadráticos dos resíduos para calcular a soma dos desvios quadráticos do modelo e nomeie esse valor como Variação Resido^2;
- faça a diferença entre a soma dos desvios quadráticos total pela soma dos desvios quadráticos dos resíduos para calcular a
Variação Explicadapelo modelo;
Tabela de Anova de um Modelo Linear
A partir da partição da variação dos desvios quadráticos explicado pela preditora (tannin) e não explicado (residuos) podemos montar uma tabela de anova da mesma forma que fizemos no tutorial Testes Clássicos: ANOVA
Tabela de Anova Dieta de Lagarta
A tabela de anova tem as seguintes colunas e linhas:
- colunas:
soma quadrática,graus de liberdade,média quadrática,Fep-valor - linhas:
Modelo,Resíduo,Total
- monte uma tabela de ANOVA com as somas quadráticas como no tutorial de anova;
Equações
Somas Quadráticas
$$SS_{TOTAL} = \sum_{i=1}^n (y_{i} - \bar{y})^2$$
$$SS_{res} = \sum_{i=1}^n (y_{i} - \hat{y_i})^2$$
$$SS_{TOTAL} = SS_{regr} + SS_{res} $$
$\bar{y}$ = média da variável resposta
$\hat{y_i}$ = valor estimado pelo modelo para $x_i$
- Calcule o p-valor associado à estatística F do modelo
Utilize no excel o valor 1- DIST.F(F, df1, df2, VERDADEIRO)12) para o cálculo do p-valor sendo F o valor da estatística F calculada, df1 o grau de liberdade da regressão (normalmente 1) e df2 o valor de graus de liberdade do cálculo dos desvios quadráticos médios dos resíduos (n - 2) que é o número de observações menos dois graus relativos ao cálculo do intercepto e da inclinação.
- calcule o $r2$ (coeficiente de determinação) da regressão 13);
- salve a planilha completa para envio no formulário.
$$ R^2 = \frac{SS_{regr}}{SS_{TOTAL}} $$
Modelo Linear: tabela de anova no R
Vamos agora fazer a tabela de Anova no R
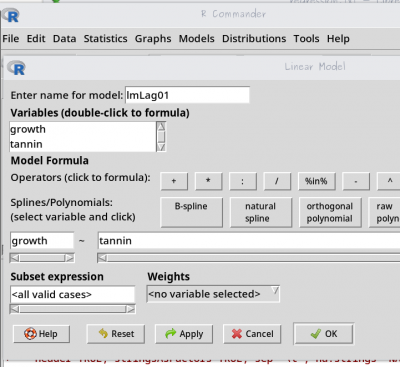
- monte um novo modelo linear, chamado
lmLag01, pelo menu (Statistics>Fit Models>Linear Models), selecione:growthcomo variável resposta;tannincomo variável preditora;
- interprete o resultado desse modelo
- faça a tabela de ANOVA do modelo gerado (
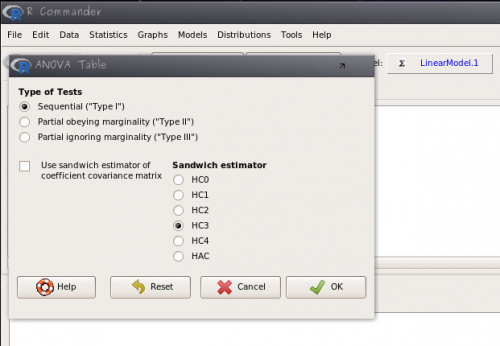
Models>Hipothesis test>Anova table); - durante o curso iremos usar a
tabela de ANOVA tipo Ionde a partição de variância é sequencial na ordem que os fatores são incluídos no modelo15); - marque a opção: Sequential (“Type I”);
- compare os valores calculados na planilha eletrônica com a tabela de ANOVA do modelo linear do Rcmdr, reconheça a partição da variação em ambos.
Modelo Mínimo
Com esses mesmos dados podemos construir o modelo denominado mínimo ou nulo. No experimento de crescimento da lagarta, a hipótese nula é que tannin não tem efeito em growth. Podemos construir o modelo que representa esse cenário, criando o modelo em que growth não tem preditoras.
- garanta que o os dados
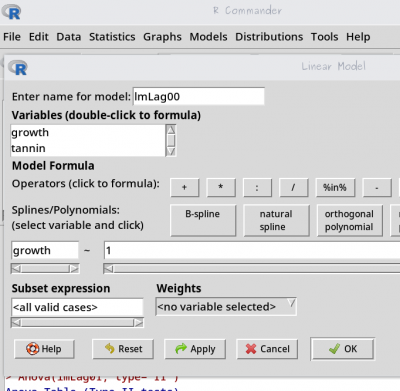
lagartaestão ativos no Rcmdr; - monte um novo modelo linear, chamado
lmLag00, pelo menu (Statistics>Fit Models>Linear Models), selecione:growthcomo variável resposta;- inclua
1,numeral um, como variável preditora16);
- monte a tabela de anova do modelo
lmLag00no menu:Models>Hipothesis tests>ANOVA table
Não há muito a ser interpretado nos resultados do modelo mínimo, mas reconheça os valores que são estimados no resultado do modelo em Coefficients Estimate. Note que neste modelo não há inclinação, pois não existe preditora. Na tabela de ANOVA verifique o valor do Sum Sq Residuals e reconheça onde ele se encontra na tabela de ANOVA montada na planilha eletrônica.
Comparando Modelos
O procedimento de partição da variação e calculo da razão entre variâncias pode ser generalizado e utilizada como critério para comparação de modelos aninhados. Modelo são considerados aninhados quando o mais complexo engloba todos as variáveis do mais simples, e por consequência, o modelo mais simples não pode explicar mais variação do que o mais complexo.
O modelo lmLag00 é aninhado ao modelo lmLag01 e por isso podemos fazer a comparação entre eles pelo critério de partição da variação como segue.
Comparando modelo com o mínimo (nulo) no Rcmdr
- confira se na caixa
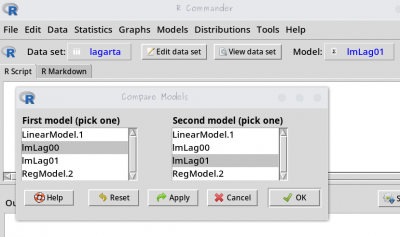
Model:existem os modeloslmLag00elmLag01; - utilize o menu
Models>Hypothesis Test>Compare two models; - na caixa que se abre selecione
lmLag00elmLag01para comparação;
- compare os valores dessa tabela de comparação entre modelos com a tabela de ANOVA do modelo
lmLag01; - reconheça os valores das partições de variação em ambos os casos.
Na comparação de modelos a razão de variância é relacionada ao quanto o modelo mais complexo explica da variação dos dados em relação ao modelo mais simples. De uma certa forma, a tabela de ANOVA no R sempre apresenta a partição da variância da comparação de dois modelos aninhados. A tabela de ANOVA de um modelo isolado é equivalente a comparar o modelo em questão com o modelo mínimo (nulo) correspondente. O entendimento desses conceitos é fundamental para utilizarmos a partição de variação como crítério para a tomada de decisão sobre qual modelo melhor explica nossos dados.
Nesse ponto, é desejável que tenha entendido que a partição da variância de um modelo é correspondente a compará-lo com o modelo mínimo (nulo), ou seja, quanta variância o modelo é capaz de explicar em relação ao modelo sem nenhuma preditora. Este modelo mínimo, representado por apenas um parâmetro, a média da variável resposta, apresenta toda a variação dos dados contida nos seus resíduos.
Diagnóstico do Modelo Linear
O diagnóstico do modelo linear é feito baseado nas premissas associadas ao modelo e para verificar a influência de cada observação na estimativa dos parâmetros do modelo. Os nossos dados precisam estar acoplados às premissas do modelo linear e não é desejável que o modelo seja definido apenas por uma ou por poucas observações influentes. As principais premissas dos modelos lineares são:
- a relação entre a variável preditora e a resposta é linear;
- a variabilidade tem estrutura de uma variável aleatória normal;
- a variabilidade na resposta é constante ao longo de toda a amplitude da preditora;
Além disso, avaliamos, para cada observação, sua alavancagem (leverage), definida pelo quanto a observação se afasta da média dos dados, e a sua influência (distância de Cook), definida como o quanto os parâmetros estimados são alterados ao se retirar esta observação dos dados.
Caso ainda tenha dúvidas sobre o diagnóstico dos modelos revisite o tutorial Regressão Linear para sedimentar o diagnóstico dos modelos lineares.
PARA ENTREGAR ANTES DO INÍCIO DA PRÓXIMA AULA
- Preencha o formulário neste link. Caso não consiga, encaminhe as repostas e documentos aos professores (planecousp@gmail.com), indicando como “Assunto”: Modelos Lineares Simples II.
lmdummy <- lm(colhe ~ dummy1 + dummy2 + dummy3 , data = colheitaDummy) ## avalie o modelo summary(lmdummy) anova(lmdummy)
- ajuste o modelo normal de anova
lmAnova <- lm(colhe~solo, data=colheita) ## avalie o modelo summary(lmAnova) anova(lmAnova)
- compare os coeficientes dos dois modelos
00 nas outras indicadoras0;0;0 1;0;0, 0;1;0 e 0;0;1 em cada indicadora representam respectivamente: alagado,arenoso, argiloso e humicoModels > Summarize model