Ferramentas do usuário
Barra lateral
cursos:planeco:roteiro:08b-lmii_rcmdr
Tabela de conteúdos
Modelos Lineares Simples II
Os modelos lineares são a base para o entendimento de todos os modelos mais complexos que iremos abordar durante este curso. Caso ainda não tenha feito o roteiro Modelos Lineares Simples I, retorne a ele.
Modelo Linear: partição da variação
Os modelos lineares podem ser analisados através do método de partição de variância que aprendemos no roteiro de Princípios da Estatística Frequentista. Caso não tenha sedimentado bem o conceito, retorne ao roteiro e reveja a videaula, isso será importante para acompanhar o restante deste roteiro. Assim como na análise de variância clássica onde a preditora é uma variável categórica, podemos particionar a variação total existente nos dados nas porções explicadas e não explicadas por uma variável contínua preditora. Esse particionamento da variação no caso de um modelo linear simples é análogo ao que acontece em uma análise de variância tradicional, com a diferença que essa última só pode ser aplicada para variáveis preditoras categóricas.
A nossa próxima atividade usa os dados de crescimento de lagartas submetidas a dietas de folhas com diferentes concentrações de taninos presente no livro The R Book (Crawley, 2012). São apenas duas variáveis, growth, o crescimento da lagarta, e tannins, a concentração de taninos. O objetivo é verificar se há relação entre o crescimento da lagarta e a concentração de taninos da dieta.
Desvios Quadráticos
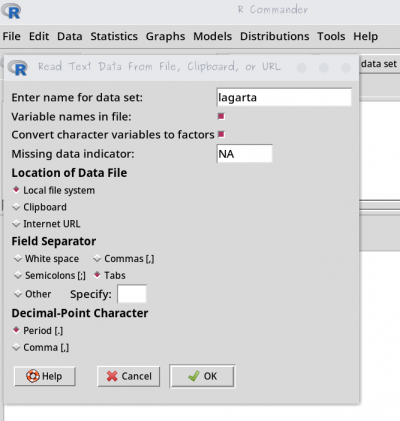
- baixe o arquivo regression.txt;
- abra o arquivo no Excel, selecionando a separação de campo como tabulação;
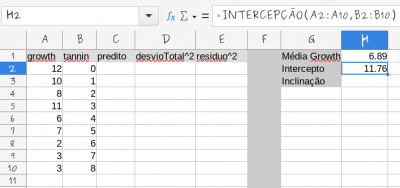
- calcule a média de crescimento das lagartas;
- calcule o intercepto e a inclinação do modelo linear no próprio excel, usando as funções descritas no quadro abaixo;
Para o cálculo dos parâmetros da reta use as funções do Excel:
- em uma coluna chamada desvio total calcule o desvio total de cada observação (o crescimento observado menos a média do crescimento);
- nomei uma coluna desvios quadráticos totais e eleve ao quadrado os valores da coluna criada anteriormente;
- some esses valores para obter a soma dos desvios quadráticos total nomeado como Variação Total
- calcule o valor predito pelo modelo em uma coluna chamada predito;
Predito pelo modelo
A predição do modelo é calculada pela equação da reta:
$$ \hat{y_i} = a + b * x_i $$
a = intercepto
b = inclinação
$x_i$ = valor de x da observação i
$\hat{y_i}$ = valor predito para a observação i
- em uma coluna chamada residuo calcule a diferença entre cada observação e o respectivo valor predito pelo modelo;
- crie uma outra coluna (residuo^2) com os valores de resíduos quadrático do modelo para cada observação (observado menos o predito pelo modelo ao quadrado);
- some os desvios quadráticos dos resíduos para calcular a soma dos desvios quadráticos do modelo e nomeie esse valor como Variação Resido^2;
- faça a diferença entre a soma dos desvios quadráticos total pela soma dos desvios quadráticos dos resíduos para calcular a
Variação Explicadapelo modelo;
Tabela de Anova de um Modelo Linear
A partir da partição da variação dos desvios quadráticos explicado pela preditora (tannin) e não explicado (residuos) podemos montar uma tabela de anova da mesma forma que fizemos no tutorial Testes Clássicos: ANOVA
Tabela de Anova Dieta de Lagarta
A tabela de anova tem as seguintes colunas e linhas:
- colunas:
soma quadrática,graus de liberdade,média quadrática,Fep-valor - linhas:
Modelo,Resíduo,Total
- monte uma tabela de ANOVA com as somas quadráticas como no tutorial de anova;
Equações
Somas Quadráticas
$$SS_{TOTAL} = \sum_{i=1}^n (y_{i} - \bar{y})^2$$
$$SS_{res} = \sum_{i=1}^n (y_{i} - \hat{y_i})^2$$
$$SS_{TOTAL} = SS_{regr} + SS_{res} $$
$\bar{y}$ = média da variável resposta
$\hat{y_i}$ = valor estimado pelo modelo para $x_i$
- Calcule o p-valor associado à estatística F do modelo
Utilize no excel o valor 1- DIST.F(F, df1, df2, VERDADEIRO)3) para o cálculo do p-valor sendo F o valor da estatística F calculada, df1 o grau de liberdade da regressão (normalmente 1) e df2 o valor de graus de liberdade do cálculo dos desvios quadráticos médios dos resíduos (n - 2) que é o número de observações menos dois graus relativos ao cálculo do intercepto e da inclinação.
- calcule o $r2$ (coeficiente de determinação) da regressão 4);
- salve a planilha completa para envio no formulário.
$$ R^2 = \frac{SS_{regr}}{SS_{TOTAL}} $$
Modelo Linear: tabela de anova no R
Vamos agora fazer a tabela de Anova no R
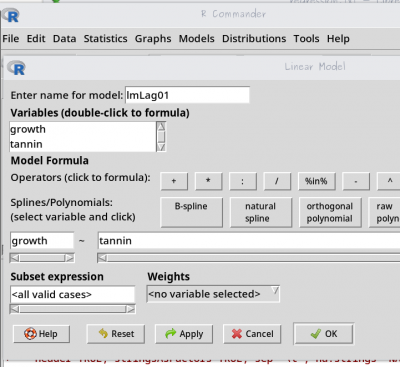
- monte um novo modelo linear, chamado
lmLag01, pelo menu (Statistics>Fit Models>Linear Models), selecione:growthcomo variável resposta;tannincomo variável preditora;
- interprete o resultado desse modelo
- faça a tabela de ANOVA do modelo gerado (
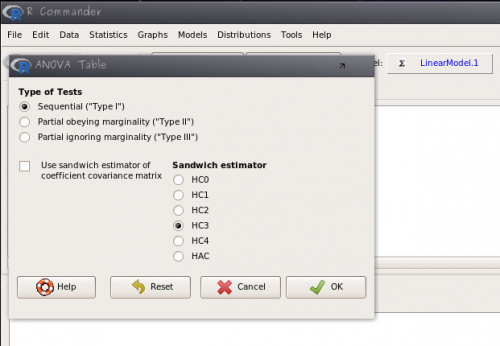
Models>Hipothesis test>Anova table); - durante o curso iremos usar a
tabela de ANOVA tipo Ionde a partição de variância é sequencial na ordem que os fatores são incluídos no modelo6); - marque a opção: Sequential (“Type I”);
- compare os valores calculados na planilha eletrônica com a tabela de ANOVA do modelo linear do Rcmdr, reconheça a partição da variação em ambos.
Modelo Mínimo
Com esses mesmos dados podemos construir o modelo denominado mínimo ou nulo. No experimento de crescimento da lagarta, a hipótese nula é que tannin não tem efeito em growth. Podemos construir o modelo que representa esse cenário, criando o modelo em que growth não tem preditoras.
- garanta que o os dados
lagartaestão ativos no Rcmdr; - monte um novo modelo linear, chamado
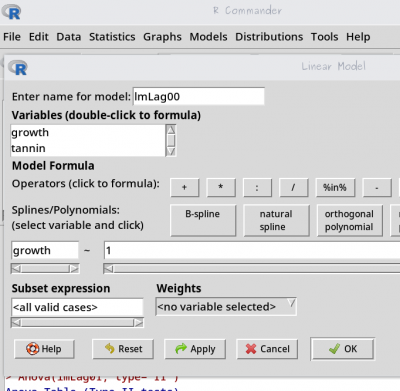
lmLag00, pelo menu (Statistics>Fit Models>Linear Models), selecione:growthcomo variável resposta;- inclua
1,numeral um, como variável preditora7);
- monte a tabela de anova do modelo
lmLag00no menu:Models>Hipothesis tests>ANOVA table
Não há muito a ser interpretado nos resultados do modelo mínimo, mas reconheça os valores que são estimados no resultado do modelo em Coefficients Estimate. Note que neste modelo não há inclinação, pois não existe preditora. Na tabela de ANOVA verifique o valor do Sum Sq Residuals e reconheça onde ele se encontra na tabela de ANOVA montada na planilha eletrônica.
Comparando Modelos
O procedimento de partição da variação e calculo da razão entre variâncias pode ser generalizado e utilizada como critério para comparação de modelos aninhados. Modelo são considerados aninhados quando o mais complexo engloba todos as variáveis do mais simples, e por consequência, o modelo mais simples não pode explicar mais variação do que o mais complexo.
O modelo lmLag00 é aninhado ao modelo lmLag01 e por isso podemos fazer a comparação entre eles pelo critério de partição da variação como segue.
Comparando modelo com o mínimo (nulo) no Rcmdr
- confira se na caixa
Model:existem os modeloslmLag00elmLag01; - utilize o menu
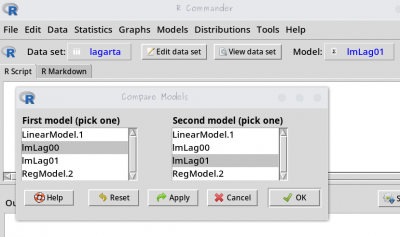
Models>Hypothesis Test>Compare two models; - na caixa que se abre selecione
lmLag00elmLag01para comparação;
- compare os valores dessa tabela de comparação entre modelos com a tabela de ANOVA do modelo
lmLag01; - reconheça os valores das partições de variação em ambos os casos.
Na comparação de modelos a razão de variância é relacionada ao quanto o modelo mais complexo explica da variação dos dados em relação ao modelo mais simples. De uma certa forma, a tabela de ANOVA no R sempre apresenta a partição da variância da comparação de dois modelos aninhados. A tabela de ANOVA de um modelo isolado é equivalente a comparar o modelo em questão com o modelo mínimo (nulo) correspondente. O entendimento desses conceitos é fundamental para utilizarmos a partição de variação como crítério para a tomada de decisão sobre qual modelo melhor explica nossos dados.
Nesse ponto, é desejável que tenha entendido que a partição da variância de um modelo é correspondente a compará-lo com o modelo mínimo (nulo), ou seja, quanta variância o modelo é capaz de explicar em relação ao modelo sem nenhuma preditora. Este modelo mínimo, representado por apenas um parâmetro, a média da variável resposta, apresenta toda a variação dos dados contida nos seus resíduos.
Diagnóstico do Modelo Linear
O diagnóstico do modelo linear é feito baseado nas premissas associadas ao modelo e para verificar a influência de cada observação na estimativa dos parâmetros do modelo. Os nossos dados precisam estar acoplados às premissas do modelo linear e não é desejável que o modelo seja definido apenas por uma ou por poucas observações influentes. As principais premissas dos modelos lineares são:
- a relação entre a variável preditora e a resposta é linear;
- a variabilidade tem estrutura de uma variável aleatória normal;
- a variabilidade na resposta é constante ao longo de toda a amplitude da preditora;
Além disso, avaliamos, para cada observação, sua alavancagem (leverage), definida pelo quanto a observação se afasta da média dos dados, e a sua influência (distância de Cook), definida como o quanto os parâmetros estimados são alterados ao se retirar esta observação dos dados.
Caso ainda tenha dúvidas sobre o diagnóstico dos modelos revisite o tutorial Regressão Linear para sedimentar o diagnóstico dos modelos lineares.
PARA ENTREGAR ANTES DO INÍCIO DA PRÓXIMA AULA
- Preencha o formulário neste link. Caso não consiga, encaminhe as repostas e documentos aos professores (planecousp@gmail.com), indicando como “Assunto”: Modelos Lineares Simples II.
1)
SLOPE no LibreOffice
2)
INTERCEPT no LibreOffice
3)
F.DIST no LibreOffice
4)
desvios quadráticos da regressão dividido pelo soma dos desvios quadrático total
5)
confira que os dados foram lidos corretamente
6)
Quando se tem mais de uma preditora é possível calcular a partição da variação em diferentes sequências, por isso existem tipos diferentes de tabelas de ANOVA
7)
esta é a forma de dizer ao R que nosso modelo não tem preditoras
cursos/planeco/roteiro/08b-lmii_rcmdr.txt · Última modificação: 2024/02/28 10:48 (edição externa)
Exceto onde for informado ao contrário, o conteúdo neste wiki está sob a seguinte licença: CC Attribution-Noncommercial-Share Alike 4.0 International
