Tabela de conteúdos
Testes Clássicos
Caso tenha feito o roteiro de testes clássicos frequentistas: Regressão Linear, passe direto para a sessão ANOVA:Análise de Variância
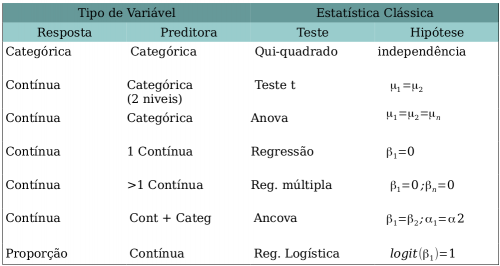
Os testes clássicos estatísticos estão inseridos no escopo da estatística frequentista ou inferência frequentista. Nessa abordagem a probabilidade é considerada uma frequência e a inferencia está baseada na frequência com que eventos ocorrem nos dados coletados. A maior parte dos testes frequentistas clássicos foi desenvolvida independentemente para a solução de problemas distintos. Por isso, não há uma unificação analítica completa, que só aconteceu posteriormente com a integração oferecida pelos modelos lineares, como veremos nas próximas aulas. Nos testes clássicos a aplicação é definida basicamente pela natureza das variáveis resposta (dependente) e preditora (independente) e pela hipótese estatística subjacente.
ANOVA: Análise de Variância
Aula Gravada - Anova: Partição da Variaçao
Esssa video aula foi gravada durante a pandemia e permanece aqui como material de referência e consulta
Na aula sobre teste de hipótese utilizamos técnicas de Monte Carlo para testar a hipótese de que duas médias são distintas, ou que uma é maior/menor que outra, tanto no exemplo do Tutorial Árvores do Mangue, quanto no exercício Altura dos alunos. Em ambos os casos estávamos comparando médias de dois grupos distintos, por exemplo, dois tipos de solos no mangue ou gênero dos alunos. O nosso procedimento foi análogo ao teste frequentista t de Student, mas a forma de obter o p-valor foi diferente. Nos procedimentos anteriores, simulamos o cenário nulo e comparamos o valor observado (diferença das médias) com a distribuição de probabilidades obtidas por meio dessa simulação. Na abordagem clássica do teste frequentista t de Student, a estatística de interesse t da amostra é comparada com a distribuição probabilística t , desenvolvida pelo matemático britânico William Gosset.
Caso não esteja confortável com o procedimento de simulação do cenário nulo e consequente obtenção do p-valor , refaça o tutorial teste de hipótese. No procedimento apresentado está a lógica básica por trás da maioria dos testes de hipótese clássicos.
A Análise de Variância ( ANOVA ), desenvolvida pelo também britânico Ronald Fisher há mais de 100 anos (1918), é uma generalização do teste t de Student. Apesar da idade avançada, é um teste muito popular, talvez o mais utilizado em ciências naturais nas últimas décadas. A hipótese subjacente da ANOVA é de diferença entre as médias de 2 ou mais grupos. O procedimento para o cálculo da estatística da ANOVA, chamada de F, está associado à partição da variância dos dados, por isso o nome. Uma maneira clássica de apresentar o resultado do teste de ANOVA é a a chamada tabela de ANOVA. Tanto a partição da variação quanto a tabela de ANOVA serão utilizados para avaliarmos outros modelos durante o curso, por isso é importante entender bem o que é a partição da variação e o que a tabela de ANOVA nos apresenta.
Partição da Variância
O teste de ANOVA está baseado na premissa de que os efeitos entre os grupos são aditivos e com isso é possível particionar a variação dos dados na porção que é associada aos grupos e a que representa a variação não explicada (resíduos ou erros). A soma destas variações resultam na variação total associada aos dados.
Para exemplificar a partição da variância associada à ANOVA, vamos usar o exemplo de dados de colheita de um cultivar em diferentes tipos de solos, apresentado no livro de Robert Crawley, The R Book, como segue abaixo:
Tradução livre da descrição do livro “The R Book” (Crawley, 2007)
“… a melhor forma de entender o que está acontecendo é trabalharmos um exemplo. Temos um experimento em que a produção agrícola por unidade de área é medida em 10 campos de cultivo selecionados aleatoriamente de cada um de três tipos diferentes de solo. Todos os campos foram semeados com a mesma variedade de semente e manejados com as mesmas técnicas (fertilizantes, controle de pragas). O objetivo é verificar se o tipo de solo afeta significativamente o rendimento de culturas, e caso afete, quanto.”1)
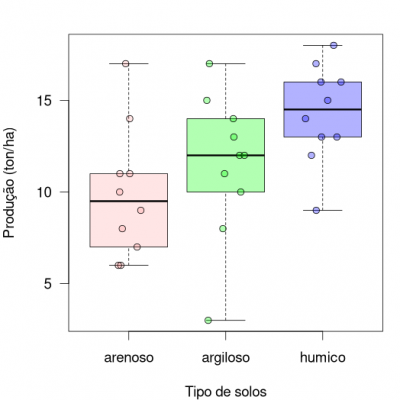
A representação gráfica desses dados pode ser feita em um boxplot.
É possível notar que há uma grande variação na produtividade entre os solos e também muita variação dentro de um mesmo tipo de solo. Para ter alguma confiança para afirmar que o solo influencia a produtividade, podemos nos basear na variação dos dados e na partição em seus componentes, ou seja, dentro de cada grupo (ou intra grupo) e entre os grupos do tratamento (tipos de solos). Primeiro vamos definir o que é a variação total dos dados.
Variação total
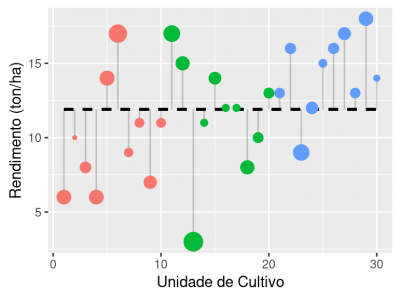 A variação total dos dados é calculada a partir dos desvios das observações (n=30) em relação à grande média 2)). No gráfico acima esta variação é representada pelos segmentos verticais em cinza. A grande média é definida como a média de produtividade de todos os campos de cultivo, independente do tipo de solo, e é representada pela linha preta horizontal tracejada.
A variação total dos dados é calculada a partir dos desvios das observações (n=30) em relação à grande média 2)). No gráfico acima esta variação é representada pelos segmentos verticais em cinza. A grande média é definida como a média de produtividade de todos os campos de cultivo, independente do tipo de solo, e é representada pela linha preta horizontal tracejada.
Medimos essa variação total pela soma quadrática definida como os valores dos desvios dos dados em relação à grande média (segmentos verticais no gráfico) elevados ao quadrado e posteriormente somados.
$$ SQ_{"total"} = \sum_{i=1}^k\sum_{j=1}^n (y_{ij} - \bar{\bar{y}})^2 $$
Variação intra grupo
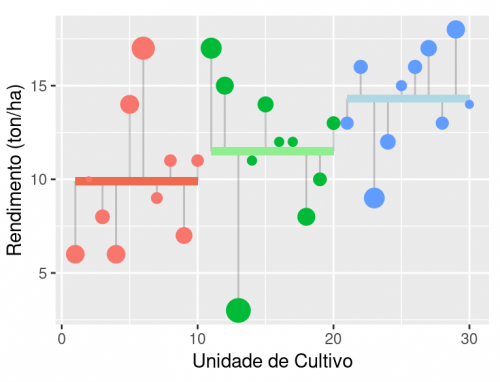 A variação intra grupo é a variação que não está relacionada ao efeito do tratamento (no caso, os tipos de solo). Essa variação é baseada nos desvios dos valores observados em relação à média do nível de tratamento (tipo de solo ou grupo) representada pelos segmentos horizontais coloridos. Os respectivos desvios estão representados na figura acima pelas barras cinza verticais.
A variação intra grupo é a variação que não está relacionada ao efeito do tratamento (no caso, os tipos de solo). Essa variação é baseada nos desvios dos valores observados em relação à média do nível de tratamento (tipo de solo ou grupo) representada pelos segmentos horizontais coloridos. Os respectivos desvios estão representados na figura acima pelas barras cinza verticais.
Entendemos desvios como qualquer variação em relação a alguma medida de tendencia central, no caso estamos tratando dessa variação em relação a diferentes médias (grande média e média dos grupos). Mais à frente iremos chamar esses desvios das observações em relação às médias do seu grupo de resíduos e muitos estatísticos também os chamam essa variação de erro. Não se assustem, eles significam a mesma coisa e causam confusão, mesmo. O importante é entender que estamos nos referindo à variação que não é explicada pelos tratamentos.
Para quantificar essa variação utilizamos a soma quadrática intra grupo, obtida a partir desses valores de desvios 3). Basta pegar a diferença entre cada valor observado em relação à média do seu grupo, elevar ao quadrado e posteriormente somar esses valores, como descrito na formula a seguir:
$$ SQ_{"intra"} = \sum_{i=1}^k\sum_{j=1}^n (y_{i,j} - \bar{y}_{i})^2 $$
Variação entre grupos
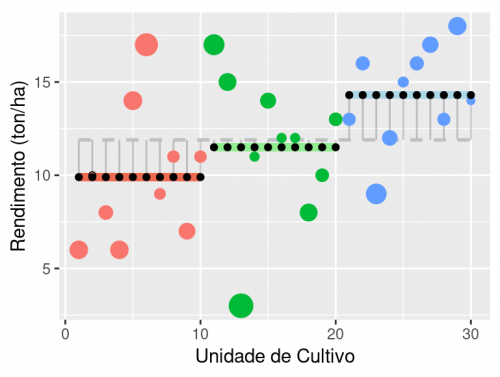 Por fim, temos a variação entre os grupos. Essa variação está diretamente relacionada ao efeito dos níveis do nosso tratamento, que no caso são os tipos de solo. Ou seja, quanto maior o efeito do tipo de solo na produtividade, maior será essa variação. Ela é definida pelos desvios das médias dos grupos em relação à grande média (segmentos verticais cinzas). Essa variação pode ser representada substituindo cada valor observado (círculos coloridos) pela média do seu grupo (círculos pretos). Os desvios desses valores médios dos grupos em relação à grande média, elevado ao quadrado e somados, representam a soma quadrática entre grupos.
Por fim, temos a variação entre os grupos. Essa variação está diretamente relacionada ao efeito dos níveis do nosso tratamento, que no caso são os tipos de solo. Ou seja, quanto maior o efeito do tipo de solo na produtividade, maior será essa variação. Ela é definida pelos desvios das médias dos grupos em relação à grande média (segmentos verticais cinzas). Essa variação pode ser representada substituindo cada valor observado (círculos coloridos) pela média do seu grupo (círculos pretos). Os desvios desses valores médios dos grupos em relação à grande média, elevado ao quadrado e somados, representam a soma quadrática entre grupos.
$$ SQ_{"entre"} = \sum_{i=1}^k\sum_{j=1}^n (\bar{y}_{i} - \bar{\bar{y}})^2 $$
Variação aditiva
Acabamos de particionar a variação dos dados de um teste de ANOVA em seus componentes básicos: a variação entre e intra grupos. Uma característica importante dessa partição é que suas partes são aditivas, ou seja, a variação total é a soma da intra e entre grupos.
$$ SQ_{"total"} = SQ_{"entre"} + SQ_{"intra"} $$
Estatística F
A grande sacada de Sir Fisher foi entender que essa partição da variância aditiva pode ser utilizada para compor uma estatística que representa o quanto a variação do efeito do tratamento é maior que a variação não explicada pelo tratamento. A estatística F é definida pela razão do valor médio da variação entre grupos e o valor médio da variação intra grupos.
Os valores médios de variação (variância) são calculados dividindo as somas quadráticas pelos graus de liberdade. No caso da variação entre grupos do nosso exemplo o total de graus de liberdades é igual ao número de grupos no tratamento menos 1 (em função do parâmetro média geral usado para o seu cálculo). Na variação intra grupos o total de graus de liberdade é igual ao número de observações (30 valores usados para o seu cálculo) menos 3 (número de parâmetros utilizados para o seu cálculo, as médias dos grupos), no caso 27.
$$MQ_{"entre"} = \frac{SQ_{"entre"}}{gl_1}$$
$$MQ_{"intra"} = \frac{SQ_{"intra"}}{gl_2}$$
$$F_{(gl_1,gl_2)} = \frac{MQ_{1}}{MQ_{2}}$$
sendo:
- F: estatística F
- gl: graus de liberdade
- ${_1}$: entre grupos
- ${_2}$: intra grupos
A probabilidade de ocorrência de valores da estatística F sob um cenário nulo segue uma distribuição desenvolvida por Sir Ronald Fisher e por George Snedecor. Essa distribuição possui dois parâmetros, os graus de liberdade entre e intra grupos. Assim, para calcular o p-valor para um dado valor de F observado no nosso estudo, usamos os graus de liberdade entre grupos e os graus de liberdade intra grupos para consultarmos uma tabela de F ou utilizarmos algum programa que tenha essa distribuição definida.
Coeficiente de determinação
Outra estatística muito utilizada, baseada na partição de variação, é o coeficiente de determinação. O coeficiente de determinação define o quanto da variabilidade dos dados é explicado pelo fator de interesse, no nosso exemplo, os tipos de solos. O coeficiente de determinação (R²) é calculado pela razão entre a variação explicada e a variação total dos dados.
$$ R^2 = \frac{SQ_{"entre"}}{SQ_{"entre"} + SQ_{"intra"}} $$
Tabela de ANOVA
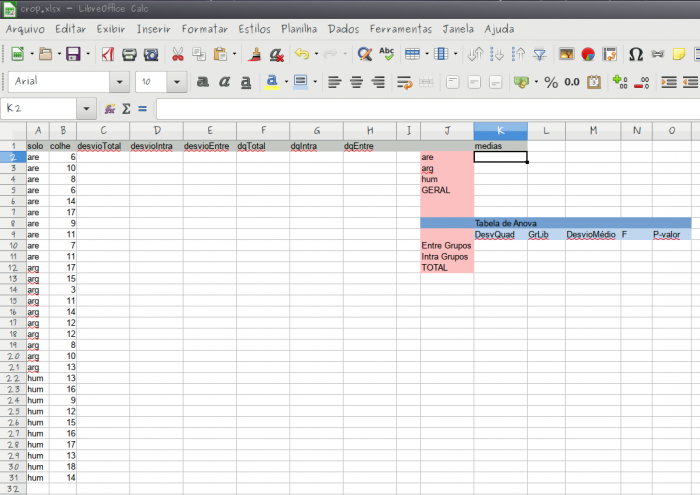
Para fixar esses conceitos vamos construir uma tabela de ANOVA em uma planilha de Excel ou LibreOffice.
- baixe o arquivo crop.xlsx;
- abra em uma planilha eletrônica;
- 1) a partir dos dados de produtividade (colheita) obtidos, calcule a média de cada grupo e a média geral e guarde nas células correspondentes à direita, na coluna K;
- 2) na coluna “desvioTotal” calcule o quanto cada observação desvia da média geral;
- 3) na coluna “desvioIntra” calcule o quanto cada observação desvia da média do seu grupo;
- 4) na coluna “desvioEntre” calcule, para cada observação, o quanto a média do seu grupo desvia da média geral;
- 5) nas colunas de desvio quadrático (dq*) correspondentes a cada coluna anterior, eleve ao quadrado cada um dos desvios calculados anteriormente.
- O que representam as somas das colunas (dq*)?
- 6) usando as orientações acima e as informações fornecidas na aula complete a tabela de ANOVA;
- 7) usando a dica abaixo, calcule o p-valor e insira na tabela de ANOVA;
Como calcular o p-valor a partir do F
- A função
DIST.Fno Excel ou LibreOffice calcula o p-valor a partir da estatística F e graus de liberdade; - usualmente a função recebe o valor de F, seguido dos graus de liberdade entre e intra grupos;
- normalmente o resultado da função
DIST.Fé a probabilidade cumulativa, mas fique atento, pode ser a densidade probabilística, dependendo do padrão do Excel. Consulte a documentação do ''DIST.F'' do Excel caso tenha dúvida; - no caso do valor retornado seja a probabilidade cumulativa, o p-valor é igual a 1 menos essa probabilidade 4).
- 8) a partir das dicas abaixo, repita o teste no Rcmdr e compare os resultados;
ANOVA no Rcmdr
- importe os dados apenas com as colunas de dados brutos;
- o menu
Statisticsestá separado em tipos de estatísticas e qual o parâmetro associado ao teste de hipótese estatístico; - o nosso teste é sobre médias, portanto no sub-menu
Mean; - nele há a opção
Multi-way ANOVA… - o resultado aparecerá na janela Output.
- 9) faça um gráfico que represente bem os dados;
- 10) interprete os resultados obtidos.
Exercício Anova
Delphinus nuttallianum
Vamos usar para esse exercício o exemplo do ótimo livro de estatística para ecólogos de Gotelli & Ellison (veja nossa lista de leituras recomendadas).
O experimento descrito analisou o efeito do degelo da primavera no crescimento e floração de uma planta alpina (Delphinus nuttallianum). Nesse experimento quatro parcelas foram mantidas sem nenhuma manipulação (unmanipulated), quatro foram aquecidas fazendo com que o degelo ocorresse antes do normal na primavera (treatment) e quatro foram manipuladas contendo toda a estrutura dos aquecedores, sem que estes fossem ligados (control). Os resultados do tempo de floração (dias) em cada parcela são apresentado abaixo:
| Unmanipulated | Control | Treatment |
|---|---|---|
| 10 | 9 | 12 |
| 12 | 11 | 13 |
| 12 | 11 | 15 |
| 13 | 12 | 16 |
- Organize esses dados em um planilha de forma que nas linhas estejam as observações e nas colunas as variáveis, no caso a reposta e preditora5). Para maiores informações sobre organização de dados em planilhas eletrônicas veja o artigo Data Organization in Spreedsheets (Broman & Woo, 2018)
- Construa a tabela de ANOVA e calcule o R² para esses dados em uma planilha eletrônica.
PARA ENTREGAR ANTES DO INÍCIO DA PRÓXIMA AULA:
Inclua os seguintes produtos no formulário abaixo:
1) Para os dados de solos e produtividade (Crawley, 2007):
- 1.1- a tabela de ANOVA completa gerada na planilha eletrônica;
- 1.2- a tabela de ANOVA resultante do teste no Rcmdr;
- 1.3- um gráfico para representar os resultados;
- 1.4- a interpretação dos resultados (máximo de 5 linhas).
2) Para os dados de Delphinus nuttallianum:
- 2.1- a tabela de ANOVA completa gerada em uma planilha eletrônica;
- 2.2- um gráfico para representar os resultados;
- 2.3- interpretação dos resultados desse experimento (máximo de 5 linhas)
- 2.4- a reposta para a seguinte questão: Por que o
unmanipulatednão é o controle para o tratamento que manipulou o degelo?(máximo 5 linhas)