Análise de Dados Categóricos
— Alexandre Adalardo 2008/12/31 13:41
Esta página wiki é baseado largamente no livro “A Primer of Ecological Statistics” de Nicholas Gotelli, mesmo autor de “A Primer of Ecology”, que dispensa maiores apresentações, com co-autoria de Aaron Ellison (the last but not the least! sorry Aaron!!).
Esse material foi produzido para uma aula introdutória sobre o análise de dados categóricos em um curso de campo, portanto bastante básica, mas pretendo incluir mais material futuramente.
Variável Categórica
O estado da variável está relacionado a diferentes níveis que pode ser ordenado ou não.
Não ordenados:
sexo (masculino,feminino, outros), ambiente (capoeira, floresta, campo), nome do fragmento (A, B, C)
Ordenados:
classes de luminosidade (alta, média, baixa),
tamanho de fragmento (pequeno, médio, grande)
Tipos de Análises
Quando a variável preditora (independente) é categórica e a variável resposta (dependente) também, analisamos os dados através de tabelas de contingência.
- Uma variável preditora temos:
- ✘2,
- teste G,
- Teste exato de Fisher
- Mais do que uma variável preditora
- OUTRA AULA
Aqui vamos tratar apenas do primeiro caso, com apenas uma variável preditora, com a premissa de que apenas uma variável é capaz de prever os resultados, ou que com apenas uma variável explica grande parte da variação encontrada nos dados.
Exemplo de dados
Em nossos exemplos utilizaremos um conjunto de dados relacionado à herbivoria (alta, baixa) de populações de plantas em dois ambientes de restinga (duna e floresta)
- Plantas da Restinga
Dado 73 populações de espécies de plantas em dois ambientes, classificamos cada população quanto à perda de área foliar(alta ou baixa).
Uma forma de apresentar uma síntese desses dados e com uso de tabela de contingência, como segue:
| AMBIENTE | ||
|---|---|---|
| Herbivoria | Floresta | Duna |
| Alta | 18 | 8 |
| Baixa | 15 | 32 |
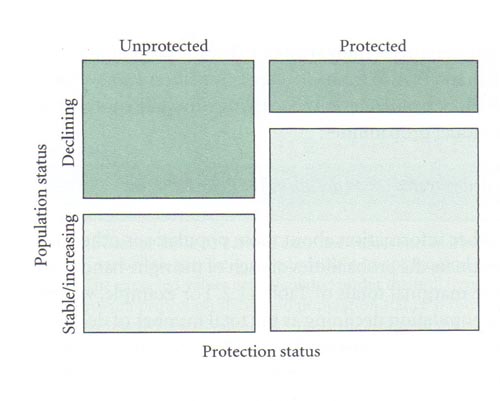
Apresentação Gráfica
Uma outra forma de apresentar esses dados é através de um gráfico de mosaicos. Nesse gráfico, como usual, o eixo x é representado pela variável preditora e o eixo y pela resposta.
As áreas nesse gráfico são proporcionais às observações em cada célula da tabela de contingência e dão ideia da contribuição de cada nível do fator no total de observações.
Hipótese
A hipótese nula em tabelas de contingência é que as variáveis preditoras e resposta são independentes. Ou seja, não há poder preditivo com relação à resposta observada. No caso em questão, a hipótese nula é que não há nenhuma relação entre o ambiente e a perda de área foliar. A nossa hipótese de trabalho nesse caso é saber se as populações de um ambiente tendem a ser mais herbivoradas que outro.
O Teste Estatístico
✘2
O primeiro passo é calcular os valores esperados para cada célula da tabela de contingência caso a hipótese nula esteja correta. Ou seja, se não há nenhuma relação entre as variáveis quais valores esperaríamos encontrar.
Vamos calcular o valor esperado das populações em relação à herbivoria, no cenário da hipótese nula:
Probabilidade de maior herbivoria: igual a frequência de alta herbivoria pelo total de observações 26/73 ou 0,356 Probabilidade de ser uma população da floresta: 33/73 ou 0,452 Probabilidade desse dois eventos ocorrerem juntos: 0,356 x 0,452 = 0,161 Valor esperado é a proporção de 0,161 do total de observacões: 0,161 x 73 = 11,75
Seriam esperados portanto, 11,75 eventos para o valor da primeira célula da tabela de contingência.
Note que as propabilidade acima são calculadas através dos totais marginais da tabela de contingência e são independentes do valor observado. Abaixo construímos a tabela de contingência com os valores esperados, o que não implica em mudanças de totais marginais.
Tabela de contingência com totais marginais e os valores esperados entre parênteses
| Ambiente | |||
|---|---|---|---|
| Herbivoria | Floresta | Duna | Total Marginal |
| Alta | 18 (11,75) | 8 (14,25) | 26 |
| Baixa | 15 (21,25) | 32 (25,75) | 47 |
| Total Marginal | 33 | 40 | 73 |
O Teste Qui-Quadrado
O clássico teste de ✘2 foi desenvolvido por Pearson, o mesmo do coeficiente de correlação, por isso o teste é chamado também de Qui-Quadrado de Pearson. O cálculo é muito simples e por isso muito popular. Precisamos apenas calcular o quanto os valores observados se distanciam do esperado. Quanto maior a soma desses valores, menor a probabilidade dessa diferença ter sido gerada pelo acaso.
✘2 = ∑ ((observado-esperado)2/esperado)
Cálculo de ✘2 para a ocorrência de herbivoria em plantas: Ho = as variáveis são independentes H1 = ambientes diferentes apresentam herbivoria diferenciada. X2 = (18-11,75)^2/11,75 + (8 - 14,25)^2/14,25 + ... X2 = 3,32 + 2,74 + 1,83 + 1,52 X2 = 9,42 Cálculo dos graus de liberdade: df= (no. linhas -1) x (no. colunas -1) df= 1 Para obter o p deve-se consultar uma tabela da distribuição do Qui-Quadrado No caso: p(9.42, 1)=0,002
Como o valor de p é pequeno, podemos rejeitar a hipótese nula de que a herbivoria não está relacionada ao ambiente.
E DAI?!
Teste G
O teste G é uma alternativa ao ✘2 e está baseado na distribuição multinominal de probabilidades. Seu cálculo é baseado na relação entre os valores observados e esperado.
G= 2 x ∑ [observado x ln(observado/esperado)]
O grau de liberdade e o p são calculados da mesma forma que o ✘2.
Para amostras pequenas há um ajuste para o calculo do G que compensar valores observados baixos que tendem a superestimar as diferenças entre valores observados e obtidos.
Teste Exato de Fisher
Tanto o teste do ✘2 de Pearson quanto o G são teste assimptóticos, ou seja aproximam-se da distribuição do ✘2 para amostras grandes. De fato, uma boa aproximação! Entretanto, Fisher desenvolveu um teste para o cálculo exato do valore de p, desde que os totais marginais da tabela de contingência sejam definidos a priori.
Quando ambos totais marginais, de colunas e linhas, são fixos, o cálculo do valor de p exato é concentualmente simples mas computacionalmente intensivo. A valor exato é a probabilidade de obter o valor observado ou valores extremos ao valore esperado, ao acaso, dado os totais marginais fixados.
Não vamos apresentar a formula aqui dado que é de dificil computação, entrentanto, calcula exatamente o valor da probabilidade acima descrita.