Ferramentas do usuário
−Barra lateral
−Tabela de conteúdos
Modelos Lineares Múltiplos III
Interação entre preditoras e Colinearidade
Neste terceiro e último roteiro sobre Modelos Lineares Múltiplos vamos inicialmente utilizar um conjunto de dados com variáveis contínuas e categóricas para realizar o procedimento de seleção de modelos e posteriormente obter e interpretar, por meio dos resumos dos modelos, os coeficientes dos parâmetros, incluindo as interações. Na segunda parte desse roteiro vamos utilizar um conjunto de dados apenas com variáveis contínuas para aprender a identificar colinearidade entre variáveis, entender os efeitos sobre a seleção de modelos e reforçar a interpretação dos coeficientes do modelo final selecionado.
Variáveis contínuas e categóricas
Peso de bebês ao nascer
 O objetivo dessa pesquisa foi saber quais fatores afetam o tamanho de bebês ao nascer, de modo que fosse possível orientar campanhas de conscientização para evitar o nascimento de bebês com baixo peso, uma vez que isso pode implicar em maiores custos e muitos riscos ao bebê devido à permanência no hospital. Três variáveis preditoras (explicadas abaixo) foram consideradas relevantes para essa pesquisa, mas também havia um interesse genuíno em saber se alguma das variáveis poderia interferir no efeito das outras.
O objetivo dessa pesquisa foi saber quais fatores afetam o tamanho de bebês ao nascer, de modo que fosse possível orientar campanhas de conscientização para evitar o nascimento de bebês com baixo peso, uma vez que isso pode implicar em maiores custos e muitos riscos ao bebê devido à permanência no hospital. Três variáveis preditoras (explicadas abaixo) foram consideradas relevantes para essa pesquisa, mas também havia um interesse genuíno em saber se alguma das variáveis poderia interferir no efeito das outras.
1. Abra o arquivo babies.csv no Rcmdr, usando tabulação(Tabs) como separador de campo
2. Ajuste um modelo contendo apenas as variáveis indicadas abaixo e todas as interações entre elas:
- variável resposta: bwt = peso do bebê (medido em “onças”)
- preditoras:
- gestation = tempo de gestação (dias)
- age = idade da mãe
- smoke: FALSE = mãe não fumante; TRUE = mãe fumante
3. Selecione o modelo mínimo plausível pelo método de simplificação para mínimo adequado (ver roteiro I de MLM)
4. Para o modelo final selecionado:
- avalie os gráficos diagnósticos
- identifique qual(is) nível(is) está(ão) representado(s) no intercepto
- interprete cada um dos parâmetros do modelo, incluindo interações, se houver
- avalie qual seria a melhor campanha para evitar que bebês nasçam com baixo peso
Colinearidade entre variáveis
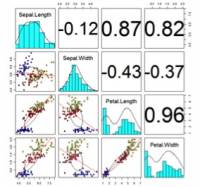 Uma importante premissa de modelos lineares múltiplos é que as variáveis preditoras sejam independentes entre si. Entretanto, em estudos observacionais ou exploratórios é relativamente comum que as variáveis preditoras não sejam independentes. Quando duas variáveis preditoras estão correlacionadas e estão explicando a mesma porção da variância da variável resposta estamos diante de um problema de colinearidade. Nos casos mais extremos, a colinearidade pode afetar a significância de algumas variáveis e até mesmo o sinal do efeito.
Uma importante premissa de modelos lineares múltiplos é que as variáveis preditoras sejam independentes entre si. Entretanto, em estudos observacionais ou exploratórios é relativamente comum que as variáveis preditoras não sejam independentes. Quando duas variáveis preditoras estão correlacionadas e estão explicando a mesma porção da variância da variável resposta estamos diante de um problema de colinearidade. Nos casos mais extremos, a colinearidade pode afetar a significância de algumas variáveis e até mesmo o sinal do efeito.
Existem várias formas de lidar com a colinearidade, mas vamos focar nossa atividade em identificar e remover variáveis que estejam inflando as estimativas de variação. Para isso, vamos usar um índice chamado de Variance Inflation Factor (VIF), que é calculado a partir dessa equação:
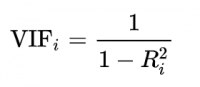
Esse R2 é obtido ajustando um modelo linear múltiplo para analisar a relação entre cada variável preditora, por exemplo i = X1, e todas as outras preditoras no modelo de interesse (X2, X3,…, Xn). Fazendo isso para todas as preditoras teremos um VIF para cada uma delas. Um alto R2 significa que grande parte da variação na preditora em questão é compartilhada pelas outras variáveis.
Quanto maior for o valor do VIF, mais os valores de erro padrão dos parâmetros do modelo serão inflados e mais dificilmente um efeito será detectado. Além da imprecisão nas estimativas dos parâmetros colineares, um outro problema que pode emergir é o modelo mínimo adequado ser diferente, dependendo da ordem da simplificação do modelo cheio. Um valor frequentemente usado para definir um limite aceitável de VIF é 4,0, acima desse valor as estimativas do modelo podem ficar comprometidas.
Nessa abordagem, após identificar quais são as variáveis com maiores valores de VIF, elas serão removidas sequencialmente. A cada variável retirada verifica-se novamente se os valores de VIF diminuíram ou se ainda precisam ser retiradas outras variáveis colineares.
Vamos ver como isso funciona na prática abaixo.
É importante entender que a escolha de qual variável retirar vai depender também do sentido biológico/ecológico de cada variável. Em alguns casos, pode valer a pena manter uma variável cujo VIF é levemente mais alto, pois o mecanismo de explicação pode ser mais explícito para essa variável.
Aves e Clima
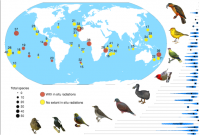
O objetivo dessa pesquisa foi avaliar quais variáveis climáticas predizem melhor a riqueza de aves em diferentes locais do mundo. Foram utilizadas 5 variáveis climáticas que são facilmente obtidas em bases de dados mundiais sobre clima.
1. Baixe o conjunto de dados birds_clim.csv 1), importe para o Rcmdr, usando vírgula como separador de campo, e visualize os dados para entender o arquivo.
2. Entenda as variáveis do arquivo:
- variável resposta: TotalBirdsRichness = Riqueza 2) total de aves registradas no local
- variáveis preditoras:
- AET = evapotranspiração real
- PET = evapotranspiração potencial
- AnnualTemperature = Temperatura média anual (em Farenheit)
- MinimumTemperature = Temperatura média mínima (em Farenheit)
- Rain = Precipitação anual (mm)
3. Inspecione a correlação entre todas as variáveis preditoras contínuas:
Para fazer isso, você tem duas opções no Rcmdr:
- Uma opção é avaliar numericamente as correlações. Para isso, entre em Estatísticas→ Resumos → Matriz de Correlação, selecione todas as variáveis preditoras contínuas e clique em OK. Você verá os valores de correlação de todos os pares de variáveis. Observando os valores mais altos de correlação, você já pode ter uma ideia se existem variáveis com potencial para apresentar colinearidade.
- Outra opção é avaliar graficamente as correlações entre as variáveis. Para isso, entre em Gráficos → Matriz de Dispersão e selecione todas as variáveis preditoras contínuas. Na aba Opções selecione “Linhas de quadrados mínimos” e clique em OK. Na figura que foi gerada, você poderá avaliar quais pares de variáveis parecem ter uma maior correlação entre elas.
Esse procedimento de analisar a correlação entre todas as nossas variáveis preditoras contínuas deveria ser sempre realizado antes de fazermos nossas análises.
4. Ajuste um modelo incluindo todas as variáveis e coloque “modbird1” como nome do modelo. Neste momento não inclua as interações. No resumo do modelo, repare nos efeitos e na significância de cada um dos parâmetros.
5. Calcule os VIFs para as variáveis incluídas no modelo
Para isso, entre em Modelos → Diagnóstico numérico → Fatores de Inflação de Variância. O primeiro resultado apresentado é uma linha com os valores de VIF para cada parâmetro do modelo. O segundo resultado apresentado é uma matriz de correlação das estimativas dos parâmetros. Note que os valores são diferentes das correlações feitas diretamente para as variáveis (item 3, acima).
Importante: Como o valor de VIF de cada parâmetro depende de quais outros parâmetros estão sendo incluídos no modelo, só é possível calcular os VIFs depois de ter ajustado um modelo. Fique sempre atento(a) se o modelo ativo é o modelo para o qual você quer calcular os VIFs.
6. Checando os valores dos VIFs:
Vamos agora checar se está claro como o VIF é calculado. Em primeiro lugar, reveja a equação de cálculo de VIF apresentada acima.
Vamos calcular manualmente o valor de VIF para uma variável preditora e comparar com o valor obtido acima no Rcmdr. Para isso, precisamos calcular o R2 da relação entre essa variável preditora e todas as outras preditoras que estavam nesse modelo (“modbird1”). Para isso, essa variável preditora na qual estamos interessados em calcular o VIF (especificamente para esse modelo completo) passará agora a ser a variável resposta de um novo modelo que criaremos. Então, vamos fazer isso para a variável AET:
Entre em Estatísticas → Ajuste de Modelos → Modelo Linear. Coloque AET como variável resposta na caixa da esquerda da equação e coloque as outras 4 variáveis preditoras na caixa da direita da equação. Defina o nome desse modelo como “vif_aet”. No resumo do modelo será apresentado um valor de R2 Múltiplo (Multiple R-square). Utilize esse valor na equação de cálculo de VIF e veja se o resultado é igual ao valor de VIF calculado pelo Rcmdr. Deveria ser. Se não foi, peça ajuda a alguém da equipe.
Repita o mesmo procedimento para outra variável de sua escolha. Você pode fazer isso para todas as variáveis do modelo, se quiser.
Continuando nossa análise…
7. Analisando o resultado dos VIFs, se houver alguma variável com valor maior que 4, ajuste um novo modelo no qual a variável com o maior VIF seja removida. Coloque “modbird2” como nome desse modelo. Olhe para o summary desse modelo e para as variáveis que permaneceram nele. Cheque os valores dos coeficientes e a significância de cada variável em relação ao modelo “modbird1”. Houve alguma alteração? Alguma variável deixou de ser significativa? Alguma variável passou a ser significativa? O sinal do efeito mudou? Depois, calcule os VIFs das variáveis do “modbird2” e veja se ainda tem alguma variável com VIF maior que 4.
8. Repita esses procedimentos até não haver nenhuma variável com VIF maior que 4.
9. Mesmo sem ter variáveis colineares, é possível que alguma das variáveis remanescentes não seja relevante para definir o número de espécies de aves. Então, agora realize o procedimento de seleção do modelo mínimo plausível pelo método de simplificação para o mínimo adequado (conforme explicado no roteiro I de MLM), usando o caminho Modelos→ Teste de hipóteses→ Comparar dois modelos no Rcmdr.
10. Avalie se entendeu os resultados do modelo final.
Exercício
No link para o formulário MLM III você deverá:
1) subir um arquivo com os resumos de alguns modelos referentes aos dados babies.csv e os gráficos diagnósticos e responder as perguntas propostas.
2) utilizar os dados de birds_clim.csv, mas agora incluindo todas as interações duplas3) entre as variáveis para ajustar um modelo “cheio”; subir um arquivo com os resumos e os gráficos diagnósticos de alguns modelos indicados no formulário; indicar quais parâmetros podem estar causando colinearidade; e interpretar o modelo final selecionado. Obs. para fazer essa análise, siga os mesmos passos indicados anteriormente, porém, no passo 7, onde lê-se “variável” leia-se “variável ou interação”

