Ferramentas do usuário
Barra lateral
Tabela de conteúdos
Modelos Lineares Múltiplos I
Uma extensão do modelo linear simples 1) são os modelos lineares com mais de uma preditora, aqui definido como modelos múltiplos. Quando temos mais de uma preditora o modelo aumenta em complexidade com mais parâmetros para estimar. Além disso, a estrutura mais complexa do modelo gera desafios para a interpretação e dificulta a avaliação da adequação do modelo aos dados. Uma primeira complexidade está relacionada a como simplificar a estrutura do modelo com a finalidade de facilitar a interpretação e melhorar a estimação dos parâmetros. A tomada de decisão sobre quais variáveis devemos reter em nosso modelo e quais podem ser retiradas, por não terem efeito na variável resposta, pode ser feita utilizando diferentes critérios e técnicas. A seguir apresentamos uma das técnicas utilizadas para essa tomada de decisão e que iremos utilizar ao longo desse curso. Outros critérios ou técnicas podem ser utilizadas com vantagens ou desvantagens em relação ao que utilizaremos. Não é objetivo desse curso se debruçar sobre essas diferentes técnicas.
Duas preditoras categóricas
O primeiro exemplo que iremos trabalhar é baseado nos dados utilizados para exemplificar o teste de Anova. Vamos criar um experimento plausível a partir dele.
Simulando um experimento plausível
Vimos que existe um efeito do tipo de solo na produção de um cultivar. Uma expectativa plausível é que a adição de adubo também tenha efeito na produtividade. Ou seja, os tipos de solo tem produtividade diferente, assim como o adubo aumenta a produtividade.
Nos dados originais do exercício de ANOVA a produtividade média nos solos foi de:
- arenoso: 9.9
- argiloso: 11.5
- humico: 14.3
Vamos, a partir dessa informação, criar um experimento onde, além da diferença do solo, metade dos cultivos foram tratados com adubo orgânico.
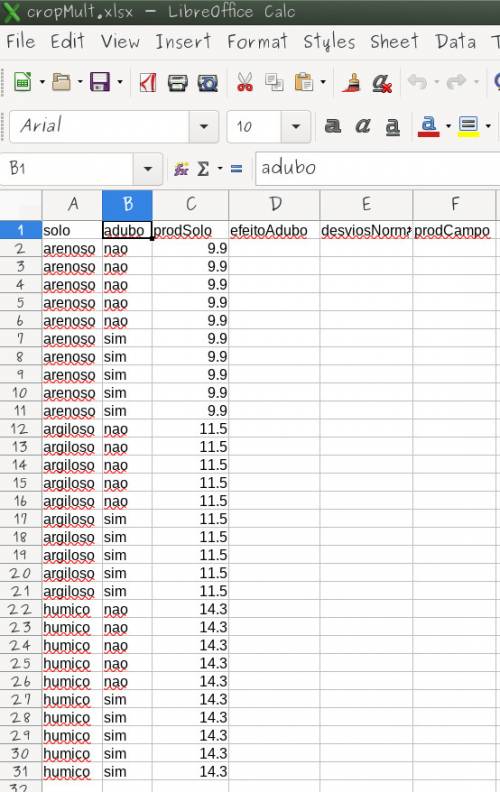
- 1. Abra o arquivo cropMulti em uma planilha eletrônica:
- 3. Preencha a célula E2 da coluna
desvios normalcom a fórmula = INV.NORM.N(ALEATÓRIO(); 0 ; 1.5)4). - 4. Some os valores em uma mesma linha
Ao final sua planilha deve estar preenchida como a que segue, apenas com os valores da coluna resíduo diferentes:
Procedimentos
- Salve a planilha com o nome
soloAduboAditivo.csvem formato texto com campos separados por vírgula; - Abra os dados no Rcmdr;
- Produza um modelo chamado
mlSolo_Adubo_Aditivoda seguinte forma:
prodCampo ~ solo + adubo;
- Avalie o modelo pelo seu sumário e pela tabela de Anova;
- Faça uma interpretação biológica do resultado do modelo.
Modelos Plausíves
O nosso modelo tem duas preditoras e pode ser simplificado. Nesse caso, como temos poucas possibilidades de comparação, podemos comparar os modelos plausíveis, desde que sejam aninhados. O que produzimos acima tem o efeito de solo e de adubo, podemos pensar em mais algumas possibilidades de modelo:
- mlSolo só com o efeito do solo:
prodCampo ~ solo
- mlAdubo só com efeito do adubo:
prodCampo ~ adubo
- mlNull sem efeito de solo ou adubo:
prodCampo ~ 1
O valor 1 na última formula indica que o modelo não tem nenhuma variável preditora 5)
Interação entre preditoras
Nos modelos acima, desconsideramos um elemento importante que emerge quanto temos mais de uma preditora, a possibilidade de uma variável preditora interferir no efeito de outra, efeito esse chamado de interação. A interação é um elemento muito importante quando temos mais de uma preditora, pois desconsiderá-la pode limitar o entendimento dos processos envolvidos. Um exemplo cotidiano da interação é visto no uso de medicamentos e o alerta da bula sobre interação medicamentosa ou efeitos colaterais para pessoas portadoras de doenças crônicas. Dizemos que um medicamento tem interação com outra substância quando o seu efeito é modificado pela presença de outra substância, como por exemplo a ingestão de álcool junto com muitos medicamentos. Nos modelos a interação tem uma interpretação similar, a resposta pelo efeito de uma variável preditora se altera com a presença de outra preditora. Muitas vezes a interação pode ser o efeito de interesse do estudo, como na pergunta: O efeito de solo na produtividade agrícola depende da quantidade de adubo orgânico adicionado? Ou em outras palavras: O efeito da adubação orgânica depende do tipo de solo? Note que nestas perguntas o foco não é se há ou não efeito do adubo ou solo, mas se a presença de uma variável afeta o efeito de outra.
- No conjunto de modelos acima, não incluímos o termo da interação. Produza o modelo abaixo incluindo o termo da interação e avalie esse modelo e seus coeficientes.
prodCampo ~ solo + adubo + solo:adubo
Não é esperado encontrar interação entre as preditoras nos dados simulados da maneira como fizemos, ele pode emergir por acaso, apenas porque temos uma variável aleatória 6). Da maneira como simulamos os dados temos duas preditoras que tem efeitos aditivos onde não há interação. Uma outra forma de dizer isso é que o efeito do adubo não interfere no efeito do solo, ou que esses efeitos são independentes. A interpretação biológica nesse caso também pode ser feita independentemente.
Simulando dados com interação
Seguindo a mesma abordagem anterior, vamos produzir dados simulando a interação entre as variáveis solo e adubo. Para isso precisamos produzir dados em que o efeito do adubo depende do tipo de solo.
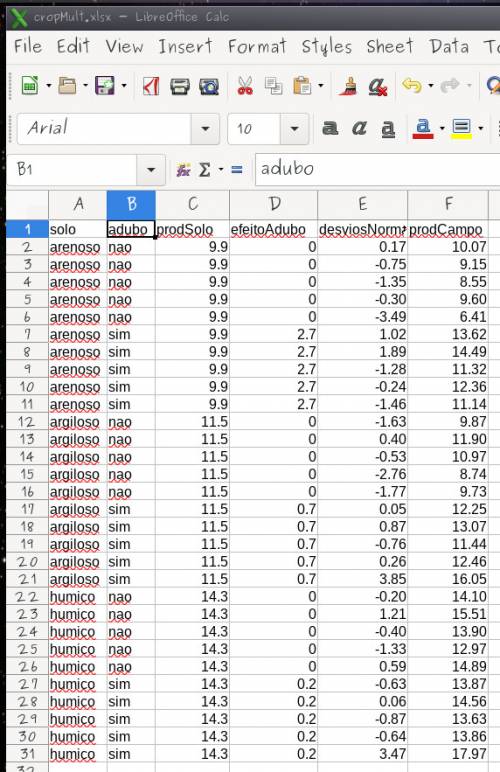
- Abra o arquivo cropMulti em uma planilha eletrônica:
- Preencha a coluna
efeitoAdubocom os valores:- 2.7 para
arenosocomaduboigual asim - 0.7 para
argilosocomaduboigual asim - 0.2 para
humicocomaduboigual asim
- O campos da coluna
efeitoAduboondeaduboé igual anãodevem ser preenchidos com0 - Preencha a célula E2 da coluna
desvios normalcom a fórmula = INV.NORM.N(ALEATÓRIO(); 0 ; 1.5)7), as atuais utilizam a mesma que o excel. - Some na coluna
prodCampoos valoresprodSolo + efeitoAdubo + desviosNormal
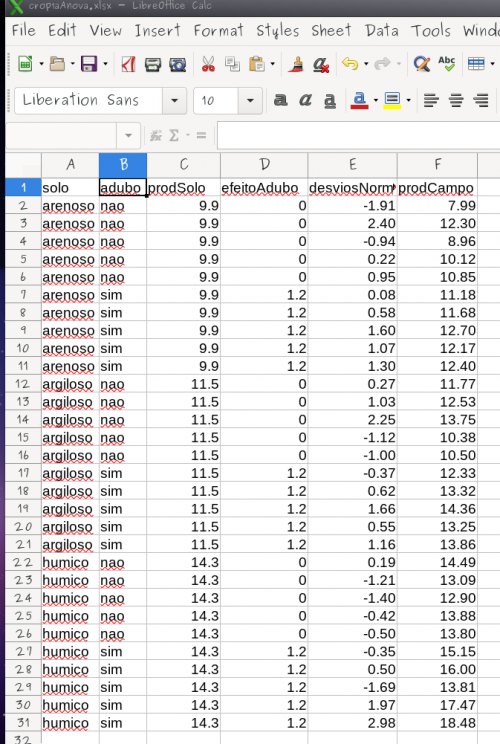
Ao final sua planilha deve estar preenchida como a que segue, apenas com os valores da coluna resíduo diferentes:
Procedimentos
- Salve a planilha com o nome
soloAduboInteracao.csv; - Importe os dados para o Rcmdr. Atenção nomeie os dados na aba de importação com o nome
soloAduboInt, em alguns casos o Rcmdr não importa se a planilha e os dados importados tiverem o mesmo nome de uma importação anterior - Confira se os dados foram lidos corretamente, inclusive se a decimal é
.; - Produza o modelo cheio
mlSolo_AduboAllcom a seguinte formula:prodCampo ~ solo + adubo + solo:adubo- interprete o resumo, comparando com o resumo do modelo similar proveniente da planilha de dados anterior
Simplificando Modelos
Durante o curso usaremos o procedimento de simplificar o modelo a partir do modelo cheio.
O procedimento consiste em comparar modelos aninhados8), dois a dois, retendo o que está mais acoplado aos dados. Para comparar os modelos utilizaremos o procedimento da partição da variância baseado na tabela de anova. Quando os modelo comparados são diferentes retemos o mais complexo, pois explica mais variação dos dados 9). Por outro lado, quando os modelos não são diferentes no seu poder explicativo, retemos o modelo mais simples, apoiados no princípio da parcimônia. Para tomar a decisão se os modelos são iguais ou diferentes utilizamos a estatística F da tabela de anova.
Princípio da parcimônia (Navalha de Occam)
- número de parâmetros menor possível
- linear é melhor que não-linear
- reter menos pressupostos
- simplificar ao mínimo adequado
- explicações mais simples são preferíveis
Método do modelo cheio ao mínimo adequado
- ajuste o modelo máximo (cheio)
- simplifique o modelo:
- inspecione os coeficientes (summary)
- remova termos não significativos 10)
- ordem de remoção de termos:
- interações não significativas (primeiro as de maior ordem)
- termos quadráticos ou não lineares
- variáveis explicativas não significativas
- caso faça sentido, agrupe níveis de fatores sem diferença
- verifique se a ordem de remoção não interfere na seleção do modelo
- retorne ao modelo cheio
- retire as variáveis que não foram retidas no outro procedimento em outra ordem
- confirme que o modelo mínimo adequado é o mesmo
- Faça o diagnóstico do modelo mínimo adequado
- Interprete o modelo selecionado
Tomada de decisão
A diferença não é significativa:
- retenha o modelo mais simples
- continue simplificando
A difereça é significativa:
- retenha o modelo complexo
- verifique se existe termo que pode e ainda não foi retirado
- caso não haja nenhum termo que possa ser retirado, este é o modelo MINÍMO ADEQUADO
Interpretando Variáveis Indicadoras (Dummy)
As variáveis indicadoras devem ser interpretadas com cuidado. No exemplo do modelo cheio acima 11), o modelo pode ser descrito da seguinte forma:
$$ y_{tr} = \alpha + \beta_1 * arg + \beta_2 * hum + \beta_3 * adubo + \beta_4 * arg * adubo + \beta_5 * hum * adubo $$
As variáveis arg, hum e adubo são dummy ou indicadoras, representadas por 1 quando presente e 0 quando ausentes. $\alpha, \beta_i$ representam as estimativas do modelo e estão relacionados, nesse caso, ao efeito de cada tratamento.
Para calcular o valor predito para o tratamento no solo arenoso com adubo, temos:
$$ y_{arenAdubo} = \alpha + \beta_3 * adubo $$
Isso em decorrência do tratamento arenoso sem adubo estar representado pelo intercepto ($\alpha$) do modelo.
Para o tratamento de solo argiloso com adubo o predito é:
$$ y_{argAdubo} = \alpha + \beta_1 * arg + \beta_3 * adubo + \beta_4 * arg * adubo $$
E assim por diante, usando as variáveis indicadoras e os coeficientes estimados para o cálculo do predito pelo modelo.
Procedimento
- Faça a seleção do modelo mínimo adequado para o conjunto de dados da última planilha, partindo do modelo com a interação, simplificando até o modelo mínimo adequado. Utilize o procedimentos de comparação de modelo pela partição de variância;
- Avalie o modelo selecionado pelo sumário e pela tabela de Anova. Reconheça os valores utilizados para gerar os dados a partir das estimativas do modelo.
- Preencha a aba
cropInterada planilha lmCrop2pred com os resultados do modelo selecionado - Na planilha onde os dados foram gerados, calcule, a partir dos coeficientes estimados, os valores preditos pelo modelo para cada uma das observações, coloque esses valores em uma coluna nomeada de
predito. Veja como calcular os valores preditos no quadro interpretando_variáveis_indicadoras_(dummy) - Calcule os resíduos do modelo 12) em uma coluna denominada
residuos - Eleve o valor dos resíduos ao quadrado em uma coluna denominada
resQuad. A soma destes valores representa a variabilidade não explicada pelo modelo - Calcule a média da variável resposta e calcule a diferença deste valor para todas as observações e eleve ao quadrado e armazene em uma coluna
desvQuadTotal, a soma destes valores representa a variabilidade total dos dados
Modelos Lineares Múltiplos: preditoras contínuas e categóricas
Nesse último tópico do bloco vamos resgatar os principais conceitos que emergiram com a generalização do modelo linear, agora com múltiplas preditoras, a partir de um exemplo com mais variáveis preditoras contínuas e categóricas.
Desafios dos modelos com múltiplas preditoras
Além da interação entre as preditoras, tratada no exemplo anterior, a inclusão de múltiplas preditoras eleva a complexidade do modelo e dificulta sua interpretação. Por exemplo, um modelo com três variáveis preditoras pode potencialmente ter quatro termos de interação14), além dos termos dos efeitos isolados. Com quatro preditoras já são 11 potenciais termos de interações possíveis. Além do número elevado de termos possíveis, as interações de níveis mais elevados são difíceis de interpretar. Essa é uma das razões para buscarmos a simplificação dos modelos antes de interpretá-los. Um outro ponto importante é nunca incluir termos no modelo que não temos capacidade para interpretar, a menos que seu modelo seja apenas preditivo. Para modelos que se propõem apenas a fazer predições, um termo complexo não impede sua aplicação. Entretanto, se a proposta do modelo é entender os efeitos causais e os processos subjacentes, um termo complexo, que não pode ser interpretado, inviabiliza o modelo. Nesses casos, é importante apenas incluir termos no modelo que são passíveis de serem interpretados.
Uma outra questão que emerge dos modelos com múltiplas preditoras contínuas é a multicolinearidade. Quando duas variável preditoras apresentam muita sobreposição de variação explicada, ou seja, ambas explicam a mesma porção considerável da variação na resposta, o modelo pode ter problemas na estimativa dos coeficientes. Além disso, modelos diferentes podem ser selecionados na busca do mínimo adequado, dependendo da ordem em que os termos são retirados ou incluídos. Variáveis com muito correlação entre elas tem grande potencial de apresentar multicolinearidade no modelo. Uma boa abordagem para quem está iniciando na modelagem estatística é investigar a correlação entre as preditoras e, caso a correlação seja muito forte, ficar atento com as estimativas do coeficientes e com a ordem de retirada dos termos do modelo ao buscar o modelo mínimo adequado. Se possível, descartar uma das preditoras colineares é uma das estratégias, já que ambas estão explicando a mesma porção da variação e são em grande parte redundantes.
Caso tenha interesse sobre outra técnica de diagnóstico de colinearidade, consulte o roteiro Modelos Lineares Múltiplos III.
Ao final desta seção é desejável que tenha compreendido nos modelos lineares múltiplos:
- a partição da variância do modelo;
- interpretar a
tabela de anovana comparação de dois modelos; - entender o procedimento da
anovapara simplificação do modelo; - interpretar os coeficientes estimados;
- entender quais níveis estão representados no intercepto do modelo;
- compreender os termos de interação;
- compor o predito pelo modelo a partir dos coeficientes;
- interpretar biologicamente o resultado do modelo;
- fazer o diagnóstico do modelo;
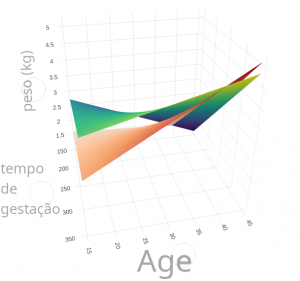
Peso de bebês ao nascer

O objetivo dessa pesquisa foi saber quais fatores afetam o tamanho de bebês ao nascer, de modo que fosse possível orientar campanhas de conscientização para evitar o nascimento de bebês com baixo peso, uma vez que isso pode implicar em muitos riscos ao bebê maiores custos devido à permanência no hospital. As variáveis preditoras consideradas para essa pesquisa estão listadas abaixo, mas também havia um interesse genuíno em saber se o efeito de uma variável poderia interferir no efeito das outras.
A descrição destes dados pode ser consultada em https://www.stat.berkeley.edu/users/statlabs/labs.html#babies.
Descrição dos dados
- variável resposta
bwt: peso do bebê ao nascer em onças(oz)
- preditoras:
gestation: tempo de gestação (dias)age: idade da mãe (anos)height: altura da mãe (polegadas)weight: peso da mãe (libras)smoke: 0 não fumante; 1 fumante
Notem que as preditoras estão relacionadas a características da mãe: dias de gestação, idade, peso, altura e se ela é fumante ou não. Como a variável resposta, peso do bebê ao nascer, foi medida em onças, vamos transformar em uma escala de medida que temos mais facilidade para interpretar, multiplicando essa variável por 0.02835 para transformar em kg. Vamos fazer o mesmo para o peso da mãe que foi medido em libras e deve ser multiplicada por 0.453592 para ser transformada em kg.
- Abra o arquivo babies.csv no Rcmdr15);
- Garanta que os dados foram lidos corretamente;
- Abra a janela para criar uma nova variável no menu
Data > Manage variables in active data set > Compute a new variable; - Na caixa
New variable namenomei a nova variável comobebeKg; - Na caixa
Expression to computecoloque a expressão:bwt * 0.02835; - Em seguida crie a variável
maeKgmultiplicandoweightpor0.453592.
Agora que temos uma variável que caracteriza o tamanho do bebê ao nascer em uma escala que faz mais sentido (kg), vamos começar a nossa avaliação de quais características da mãe tornam os bebês mais susceptíveis a nascerem com pesos baixo.
Para simplificar nosso exemplo, vamos deixar de lado duas variáveis preditoras que foram coletadas nesse estudo: parity e height. Ao final ficamos com quatro variáveis preditoras:
gestation, age, maeKg e smoke
Um mal começo
Um procedimento de modelagem ineficiente é colocar todas as variáveis preditoras e suas interações e torcer para ter alguma resultado interessante. No caso do peso dos bebês, que é razoavelmente simples com quatro variáveis preditoras sendo uma delas categórica, o modelo resultante é bastantes complexo. Vamos construir esse modelo e verificar o resultado:
No menu Estatísticas > Ajustes de modelos > Modelo linear…, construa o modelo lmFull com todas as quatro preditoras 16) e suas interações. O modelo resultante tem a seguinte expressão:
bebeKg ~ age * gestation * maeKg * smoke
Na linguagem R os símbolos de * em expressões de notação de modelos representa tanto a variável isoladamente quanto as interações possíveis.
Verifique o resumo do modelo gerado.
Um modelo como o construído acima tem muitos problemas. Nesse caso, foram estimados 16 coeficientes um para cada termo do modelo. Note também que nenhum dos coeficientes estimados é significativo nos testes marginais, ou seja, as incertezas nas estimativas dos coeficientes não nos permite afirmar que nenhum deles seja diferente de zero. Portanto, temos um modelo estatístico complexo, com 16 termos, sendo que todos os termos são multiplicados por coeficientes não distintos de zero!
Complexidade das interações
Vamos calcular o número de interações possíveis em modelo com 4 preditoras:
Combinatória
Combinatória é a operação matemática para calcular de quantas maneiras conseguimos organizar ou combinar um conjuntos de elementos. No nosso caso, temos 4 variáveis e podemos nos perguntar de quantas formas podemos combinar esses elementos em diferentes conjuntos de dois a dois (interação dupla) ou três (interação tripla) e quatro (interação quadrupla)17). A expressão matemática para essa operação é:
$$C^{r}_{n} = \frac{n!}{r! (n-r)!} $$
onde: n: número total de elementos r: número de elementos combinados
A expressão ! é a operação fatorial na matemática.
Para calcular o número de combinações possíveis de grupos de 2 e 3 elementos para um total de 4, temos:
$$C^{2}_{4} = \frac{4!}{2! (4-2)!} = 6$$ $$C^{3}_{4} = \frac{4!}{3! (4-3)!} = 4$$ $$C^{4}_{4} = \frac{4!}{4! (4-4)!} = 1$$
A lista de interações triplas e quadruplas tem essas expressões:
gestation:age:maeKg:smokeTRUEage:gestation:maeKgage:gestation:smokeage:maeKg:smokegestation:maeKg:smoke
As interações duplas:
age:gestationage:maeKgage:smokegestation:maeKggestation:smokemaeKg:smoke
Além dessas, temos os termos isolados para cada variável e o intercepto do modelo, totalizando os 16 termos do modelo lmFull.
Se tivéssemos mais uma preditora contínua em nosso modelo o número de interações possíveis subiria para 26 e o total de termos do modelo para 31.
Note que mesmo com poucas variáveis as possibilidade de interações e grande para decidirmos o que será incluído no modelo. Esse processo não é trivial e deve estar embasado no conhecimento prévio do sistema e na teoria para definir aquilo que faz sentido e pode ser interpretado, caso seja mantido no modelo.
Vamos agora comparar esse modelo cheio com o modelo sem nenhuma preditora.
Comparação com o modelo nulo
- Produza o modelo nulo chamado
lmNullcom a formula:bebeKg ~ 1
- compare com o modelo cheio produzido acima
lmFullutilizando a função:anova(lmNull, lmFull)
Nosso modelo lmFull, apesar de não ter nenhum termo com coeficientes significativamente diferentes de zero, explica uma porção razoável e “significativa” da variação dos dados. Por volta de 25% da variação dos dados é explicada pelo modelo, por outro lado, não temos nenhum termo do modelo que valha a pena interpretar. Um poder de predição razoável mas com nenhum poder de interpretação dos processos subjacentes.
Faça uma tentativa de interpretar o que o termo mais complexo deste modelo, a interação que aparece na última linha dos coeficientes estimados, está informando:
age:gestation:maeKg:smoke[T.TRUE]
O que significa uma interação entre as características da mãe: idade, dias de gestação, altura e que é fumante? Normalmente, conseguimos interpretar interações de segundo nível (levando em conta duas variáveis), algumas poucas vezes há sentido em interpretar a interação de três preditoras. Então o primeiro passo é retirar qualquer termo de interação de ordem mais alta.
Definindo as interações
Para modelos com várias variáveis preditoras é sempre complicado definir quais interações devem ser contempladas. E como vimos acima, a estimativa e a interpretação dos coeficientes do modelo ficam comprometidos. Se a intenção do modelo é entender os processos causais da variação na variável resposta, é importante iniciarmos a seleção do modelo mínimo adequado com um modelo cheio que contemple apenas os termos que são importantes para o processo em questão.
Modelo Cheio
Depois de definir quais são os termos que queremos incluir no nosso modelo (variáveis simples e interações), podemos iniciar o procedimento de modelagem seguindo algum protocolo para chegar ao modelo mínimo adequado. No nosso caso, iremos partir do modelo cheio, simplificar até o mínimo adequado. Como não temos experiência prévia do sistema e não temos “muita” experiência sobre tamanhos de bebês ao nascer, “consultamos vários especialistas na área” e eles chegaram à conclusão que os termos que deveriam ser contemplados são:
bebeKg ~ gestation + age + maeKg + smoke + gestation:age + gestation:smoke +
age:maeKg + age:smoke + maeKg:smoke + gestation:age:smoke
Seleção do mínimo adequado
- No menu
Estatísticas > Ajustes de modelos > Modelo linear…, construa o modelo com a seguinte expressão:
bebeKg ~ gestation + age + maeKg + smoke +
gestation:age + gestation:smoke +
age:maeKg + age:smoke + maeKg:smoke +
gestation:age:smoke
- simplifique esse modelo até o mínimo adequado;
Durante o processo de simplificação, quando nos defrontamos com vários termos de mesma ordem não significativos, um bom procedimento é retirar um deles de cada vez e, mesmo que o termo não seja retido no modelo, retorna-lo ao modelo antes de retirar o outro. Caso a ordem de retirada não torne nenhum dos termos significativos, ambos podem ser retirados. No caso de serem mais do que dois termos de mesma ordem, é importante também testar a retirada de dois a dois termos depois do procedimento de retirada de um a um não ter tornado nenhum termo significativo. Isso garante que a ordem de retirada não define o termo que será retido no modelo. Lembre-se que um termo “não significativo” em um modelo mais complexo pode se tornar “significativo” em um modelo mais simples.
- qual a predição do modelo selecionado do peso do bebê das seguintes mães:
- 26 anos, 280 dias de gestação, peso 55 kg e não fumante
- 26 anos, 280 dias de gestação, peso 55 kg e fumante
- 26 anos, 210 dias de gestação, peso 55 kg e não fumante
- 26 anos, 210 dias de gestação, peso 55 kg e fumante
- 26 anos, 280 dias de gestação, peso 70 kg e não fumante
- 26 anos, 280 dias de gestação, peso 70 kg e fumante
- 26 anos, 210 dias de gestação, peso 70 kg e não fumante
- 26 anos, 210 dias de gestação, peso 70 kg e fumante
- faça as mesmas predições acima, agora para uma mãe com 35 anos;
- coloque as características da mãe e as predições do modelo para os casos acima em um planilha 18);
- interprete o resultado do modelo biologicamente.
Tamanho e sobrepeso da mãe
Um “outro especialista”, ao analisar o modelo mínimo adequado selecionado acima, afirmou que a variável height deveria ser incluida para controlar o peso do bebê ser maior apenas porque a mãe era grande. Além disso, sugeriu incluir uma nova variável que indicasse a quanto a mãe tem de sobrepeso ou subpeso antes de engravidar. Indicou ainda que uma forma de criar essa variável seria utilizar os resíduos de uma regressão simples da variável peso como resposta e a variável altura como preditora. Todos os “outros especialistas” concordaram que eram uma boa sugestão, já que essa nova variável representa o quanto a mãe tem mais peso ou menos peso do que esperado para uma mãe com a mesma altura.
- inclua a variável
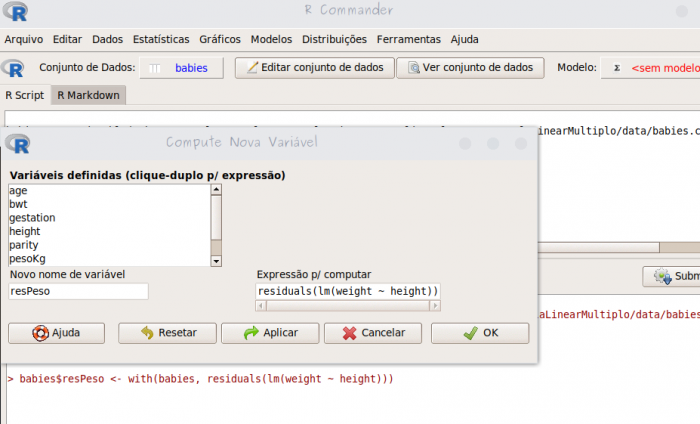
heightno modelo mínimo selecionado anteriormente e verifique se deve se essa variável deve ser retida no modelo, com a comparação dos modelos pela partição da variação; - crie uma nova variável
resPesocom a expressãoresiduals(lm(weight ~height));
- construa um modelo que inclua a variável
resPesocomo o primeiro termo no modelo mínimo adequado selecionado no procedimento anterior; - cronstrua um segundo modelo que inclua
resPesoagora como o último termo no modelo mínimo adequado selecionado nos passos anteriores; - compare os resumos de ambos os modelos e anote as diferenças encontradas;
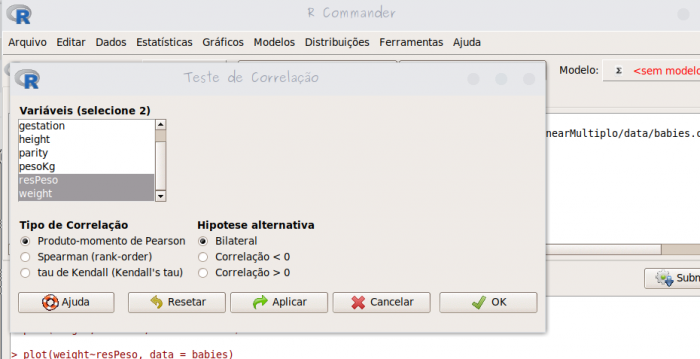
- no menu
Estatísticas>Resumos>Teste de correlaçãoselecione as variáveisresPesoemaeKg, anote o valor da correlação entre essas variáveis;
- a partir da avaliação da correlação acima tome a decisão de reter ambas, uma ou nenhuma das duas variáveis do passo acima, justifique sua decisão e construa o modelo resultante;
- simplifique o modelo do item anterior para o mínimo adequado, caso necessário;
- faça uma interpretação biológica do modelo final.
Formulário de resposta
Responda o o formulário MLM I incluindo arquivos de resultados quando solicitado.
adubo igual a simadubo igual a não = NORM.INV(RAND(), 0, 1.5) = NORM.INV(RAND(), 0, 1.5)solo e adubodesQuadTotal - resQuad) sobre a desvQuadTotal. Ou seja, quanto da variação dos dados é explicada pelo modelo em relação ao total de variação dos dadosgestation, age, maeKg e smokedata.frame, exportando depois como csv