Ferramentas do usuário
Barra lateral
Tabela de conteúdos
Modelos Lineares Mistos (LMM)
Objetivo desse roteiro
Ao final que você seja capaz de:
- 1. Entender o que são efeitos fixos e aleatórios.
- 2. Compreender a estrutura básica de um modelo linear misto.
- 3. Fazer uma análise de modelo misto no Rcmdr usando o pacote
lme4(Bates et al. 2014) - 4. Entender o output da função
lmer. - 5. Decidir quais efeitos aleatórios e fixos manter no seu modelo final.
- 6. Interpretar o resultado de um modelo misto selecionado.
Modelos Lineares Mistos (LMM)
Os modelos Lineares Mistos são uma generalização de modelos lineares que afrouxam uma premissa básica de todos os modelos que vimos até agora: a independência entre as observações. Essa falta de independência emerge por vários motivos em experimentos e muitas vezes são desejáveis pois controlam fatores de confusão. Entre as principais fontes de onde emergem essas dependências estão:
- espacial
- temporal
- biológicas
No primeiro caso, é esperado que objetos que estão mais próximos sejam mais parecidos entre si do que objetos mais longe, pois compartilham muitas condições associadas ao mesmo espaço. Dependências temporais emergem principalmente quando medimos um mesmo objetos de estudo em diferentes momentos. As biológicas estão relacionadas ao compartilhamento de caracteres ou funcionalidades entre indivíduos mais relacionados geneticamente, por exemplo.
Essa dependência portanto, cria agrupamentos de observações que compartilham similaridades que não são compartilhadas com observações de outros grupos.
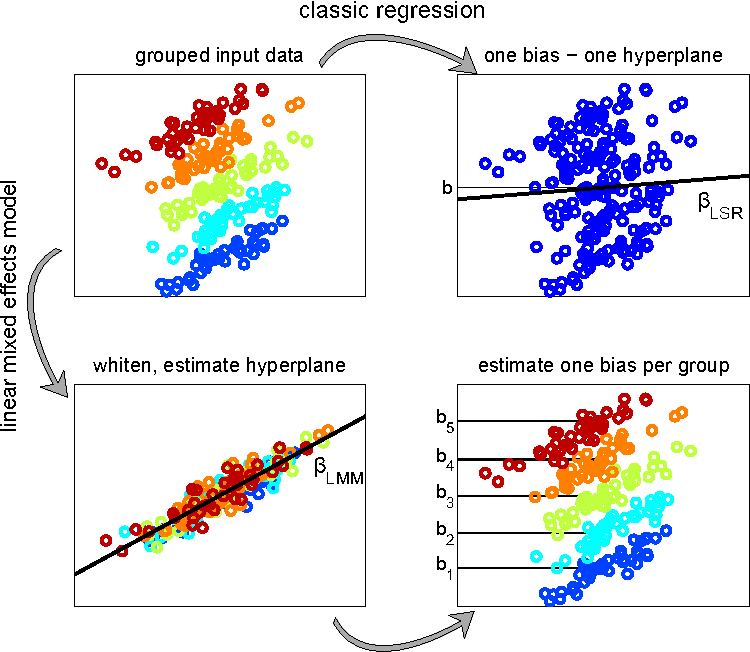
Em geral, não estamos interessados nas diferenças que existem entre esses grupos, mas precisamos contemplar a falta de independência de alguma forma. Os Modelos Lineares Mistos justamente lidam com essas falta de independência desse agrupamentos de observações. Para isso, os LMM incorporam uma estrutura aletoria adicional nos modelos lineares para acomodar esses agrupamentos definidos agora como variáveis categóricas preditoras aleatórias. Diferente das variáveis categóricas preditoras fixas onde o interesse é interpretar as diferenças entre os níveis, nas aleatórias queremos apenas estimar a variabilidade associada aos agrupamentos.
Variáveis categóricas fixas ou aleatórias
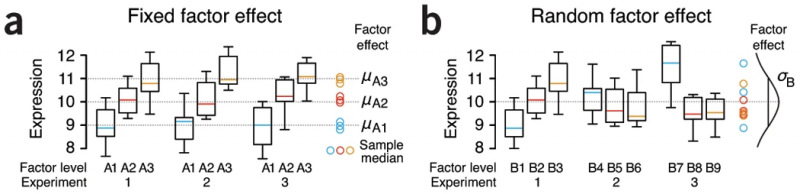
Uma forma de diferenciar as variáveis categóricas fixas e aleatórias é imaginar a realização de múltiplos experimentos, que está por trás da teoria da estatística frequentista. Em um experimento usual com a variável categórica fixa estamos interessados na estimativa das médias para cada nível da variável e buscamos saber se esses níveis são diferentes em média, como exemplificado na primeira realização do experimento (1) no painel da esquerda (a) da figura acima. Ao refazer o mesmo experimento, iriamos recoletar os mesmos níveis (experimentos 2 e 3 ) e estimar valores de médias muito próximos, como exemplificado no painel a da figura acima no seu canto direito. Por outro lado, quando temos uma variável categórica aleatória não estamos interessados em nenhum nível específico e outro experimento iria coletar outros níveis aleatórios 1) dentro todos os níveis possíveis dessa variável categórica, como mostra o painel b da figura acima. Neste caso, estamos interessados, não na diferença das médias entre os níveis e sim, na variabilidade associada à população de níveis dessa variável categórica, como mostrado no canto direito do painel b.
O vídeo abaixo apresenta uma breve introdução sobre os modelos lineares mistos .
Crescimento de Árvores
Vamos contextualizar os LMM a partir de um exemplo e suas diferença com os modelos LM. O interesse do estudo do exemplo a seguir foi entender se a deciduidade (perda de folha síncrona) de árvores está relacionada ao crescimento do indivíduo. Algumas árvores perdem as folhas de forma sincronizada (decíduas), enquanto outras trocam de folhas ao longo do tempo sem haver essa sincronicidade (perenes).
A pergunta: árvores decíduas crescem menos que árvores não decíduas? Tem seus desafios e fontes de confusão. Um complicador é que o crescimento está diretamente relacionado com o tamanho da árvore. Por isso, os pesquisadores decidiram incluir o tamanho da árvore como uma preditora fixa e com isso condicionaram o crescimento à variável tamanho. Além disso, a perda de folha síncrona é característica da espécie e eles precisaram incluir essa variável no desenho experimental.
Ao final, os pesquisadores selecionaram 5 espécies decíduas e outras 5 perenes e, para cada espécie anotaram o crescimento de 10 indivíduos, totalizando 100 indivíduos.
Deciduidade em Árvores
Vamos iniciar nosso exemplo com uma análise de modelo linear simples, sempre testando a hipótese que o crescimento de árvores decíduas e perenes é diferente.
Cresce árvores: modelo linear
- baixe os dados do experimento cresce arvores;
- faça o modelo
cresc ~ alt + dec + alt:dec; - simplifique até o mínimo adequado;
- interprete o modelo selecionado.
Procedimento em duas etapas: cresce árvores
O problema com o modelo que fizemos acima é que desrespeitamos uma pressuposto muito importante para os modelos lineares: a independência entre as observações . Os indivíduos de uma mesma espécie podem compartilhar características que poderiam fazer o crescimento de todos os indivíduos desta espécies crescer mais ou menos, independente se a espécie é decídua ou não. Por essa razão precisamos tratar essa dependência entre as observações associada aos indivíduos serem da mesma espécie. Antes de termos a instrumentação dos modelos mistos ou outras técnicas para lidar com essas dependências, uma forma de tratar as dependências entre observações era a redução da informação, por exemplo a média, para cada nível de agrupamento desta dependência, no caso aqui ilustrado, para cada uma das espécies. Como temos o crescimento dependendo do tamanho do indivíduo, a média aqui não seria uma boa redução de informação pois poderíamos ter amostrado indivíduos maiores em um espécie e menores em outra, simplesmente por acaso. Para esse caso, o que podemos fazer é a redução da relação cresc ~ alt para cada espécie e em seguida testar se as inclinações das espécies decícuoas são diferentes das espécies perenes. Se as inclinações não forem diferentes, ainda resta testar se os interceptos são diferentes. Vamos fazer esse teste.
- para cada uma das 10 espécies faça o modelo
cresc ~ alt; - guarde os coeficientes de inclinação e intercepto para cada uma das espécies junto a informação se é decídua ou perene;
- faça o modelo que testa se a inclinação é diferente entre decíduas e perenes;
- caso o a inclinação não seja significativamente diferente entre os dois grupos, faça o mesmo para a intercepto;
- interprete o resultado.
LMM: cresce árvores
Vamos agora modelar esses dados com o modelo linear mistos. O misto vem da ideia de incorporar variáveis fixas e aleatórias como preditoras. Nestes modelos a estrutura aleatória preditora pode influenciar o intercepto ou a inclinação 2). A influência no intercepto significa que a estimativa de interceptos para as espécies provêm de uma distribuição normal de interceptos definidos por um intercepto médio e um dado desvio padrão. A expressão geral para um modelo com uma preditora e a variável aleatória afetando apenas o intercepto é:
$$ y_{ij} = (\bar{\alpha} + \epsilon_j) + \beta x_{ij} + \epsilon_{ij} $$
$$ \epsilon_j = N(0, \sigma_{entre}) $$
$$ \epsilon_{ij} = N(0, \sigma_{intra}) $$
O $\bar{\alpha}$ é o intercepto médio e o $\sigma_{entre}$ é a estimativa do desvio padrão associado à distribuição de interceptos para a variável aleatória. Ou seja, no nosso caso, a estimativa da variabilidade de interceptos associado às espécies.
O modelo em que a variável aleatória influencia a inclinação tem a seguinte expressão:
$$y_{ij} = (\bar{\alpha} + \epsilon_{\alpha_j}) + (\bar{\beta} + \epsilon_{\beta_j}) x_{ij} + \epsilon_{\text{res}_{ij}}$$
Note que não ao influenciar a inclinação, por consequência o intercepto também é influenciado pela variável aleatória. Neste caso o modelo estima o intercepto médio, a inclinação média e os seguintes desvios padrão:
$$ \epsilon_{\alpha} = N(0, \sigma_{\alpha}) $$ $$ \epsilon_{\beta} = N(0, \sigma_{\beta}) $$ $$ \epsilon_{\text{res}} = N(0, \sigma_{\text{res}}) $$
LMM no Rcmdr
Existem vários pacotes disponíveis no R para realizar análises de modelos mistos. Neste roteiro usaremos o lme4 (Bates et al. 2014), que possui funções para analisar modelos lineares mistos, modelos lineares mistos generalizados e modelos mistos não lineares.
Desde o ano de 2020, os modelos mistos passaram a ser contemplados no Rcmdr. Por isso, podemos utilizar essa interface para fazer os modelos. Nas versões recentes do Rcmdr o pacote lme4 é carregado por padrão quando se constroi um modelo misto. Caso ele não seja carregado automaticamente, é possível carregá-lo. Para isso, vá em Tools → load packages e escolha lme43).
Para criar o nosso modelo cheio no R com a variável aleatória influenciando a inclinação, a notação é:
lmer(cresc ~ alt + dec + alt:dec + (alt|sp))
A expressão (alt|sp) está indicando que a variável aleatória sp irá modelar a inclinação da variável contínua alt.
O modelo em que a variável sp influência apenas o intercepto é construído com a seguinte expressão:
lmer(cresc ~ alt + dec + alt:dec + (1|sp))
O código (1|sp) indica que a variável sp vai influenciar apenas o intercepto.
Selecionando a estrutura aleatória do modelo
Assim como na estrutura fixa do modelo podemos reduzir a estrutura aleatória ao mínimo adequado para interpretar. Para isso, seguimos o procedimento descrito em Zuur et al. 2009 4).
- defina estrutura cheia das variáveis fixas;
- inicie com a forma mais complexa da estrutura aleatória;
- compare modelos aninhados por simplificando a estrutura aleatória;
- utilize a função
anovacom o argumentorefit = FALSEquando comparar modelos com diferentes estruturas aleatórias; - finalize a simplificação da estrutura aleatória 5),
- faça a simplificação da estrutura fixa do modelo como em um modelo
lm, mantendo a estrutura aleatória da forma que foi selecionada nos passos acima.
Atividade
- baixe o arquivo de dados de crescimento de árvores 6);
- leia o arquivo de dados no Rcmdr;
- construa o modelo cheio;
- faça a simplificação do modelo seguindo os passos indicados acima;
- interprete o modelo selecionado.
PARA ENTREGAR ANTES DA PRÓXIMA AULA Acesse o formulário e responda às questões propostas referentes aos dados sobre crescimento de árvores.
Riqueza em praias
Esse exemplo no roteiro é baseado em material desenvolvido por alunos de nosso programa de PG 7)Melina Leite, Marília Gaiarsa e Lucas Medeiros e vem sendo modificado, ao longo dos anos, para adaptá-lo ao curso.
Para exemplificar o que são modelos mistos e sua importância em ecologia, usaremos como exemplo um conjunto de dados presente no capítulo 5 de Zuur et al. (2009). Esses dados são referentes a um estudo sobre a riqueza de espécies da macrofauna em 9 praias na costa da Holanda. Em cada uma das praias os autores coletaram dados em cinco localidades diferentes. Para cada localidade existe informação sobre a altura da estação de amostragem em relação à altura média da maré (NAP, variável contínua) e também um índice de exposição da praia (Exposure, variável categórica).
Vamos supor que estamos interessados em verificar se a altura em relação à altura média da maré (variável NAP) influencia a riqueza de espécies nessas praias, deixando de lado a variável de exposição nesse momento. Podemos, por exemplo, construir um modelo linear simples da seguinte forma:
$$\text{riqueza} = \alpha + \beta * \text{NAP} + \varepsilon$$
sendo que $\varepsilon$ é o resíduo com distribuição normal (ou gaussiana) de média zero e um dado desvio padrão:
$$ \varepsilon = N(0, \sigma) $$
Aqui estamos modelando a riqueza de cada ponto de amostragem em função da variável NAP. O coeficiente $\alpha$ é o intercepto do modelo, $\beta$ é a inclinação (coeficiente angular ) de NAP, que definem a esperança (média) do modelo. O resíduo do nosso modelo ($\varepsilon$) é a variação da riqueza que não conseguimos explicar com nossa variável preditora NAP. Este é o escopo dos modelos lineares que estudamos até o momento.
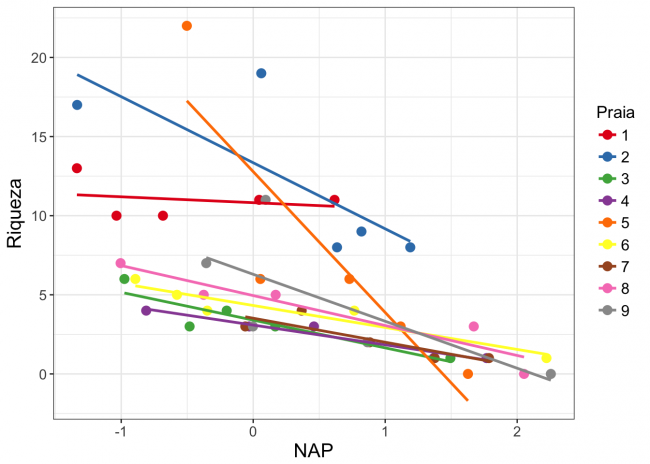
No entanto, neste exemplo o modelo viola uma premissa fundamental de modelos lineares, a de que as observações que geram os dados são independentes umas das outras (Winter, 2013). Os dados obtidos em uma mesma praia não são independentes entre si (dependência espacial). É possível imaginar diversas características particulares de cada praia, como o tipo de grão de areia ou a inclinação da praia, que podem influenciar a riqueza de espécies e que não estão contempladas nesse modelo. Deste modo, os valores de riqueza obtido pelas unidades amostrais de uma mesma praia tendem a ser mais parecidos entre si, independente da relação com as variáveis preditoras que estamos analisando. Veja o gráfico abaixo, em que cada cor representa uma praia, para avaliar visualmente se a relação entre riqueza e NAP é diferente entre praias:
Nesta figura temos as retas do modelo linear simples entre Riqueza e NAP aplicado para cada praia . Entretanto, a pergunta do estudo não diz respeito a cada praia separadamente, o objetivo é modelar a relação para todas as praias amostradas, sem especificar o que acontece para cada praia isoladamente. Por outro lado, se considerarmos cada ponto de amostragem como se fossem independente entre si, estaremos incorrendo em um erro denominado de pseudo-replicação ou falta de independência das observações8). Ou seja, queremos considerar essa dependência sem falar especificamente de nenhuma praia e, ao mesmo tempo, avaliar a variação associada às praias. Além disso, queremos que as praias amostradas representem uma amostra aleatória de todas as praias que poderíamos contemplar no nosso estudo.
Efeito Aleatório: riqueza em praias
Para isso, precisamos de um modelo linear que incorpore o fato de que nossos dados estão agrupados em praias. Chamamos de efeito aleatório uma variável que agrupa nossos dados e que, geralmente, seu efeito sobre a variável resposta não nos interessa diretamente 9). Nesse exemplo, os autores amostraram 9 praias, mas poderiam ter feito o mesmo estudo amostrando outras 9 praias em uma amostra aleatória. Nesse sentido, as 9 praias da amostra são apenas 9 possíveis praias amostradas aleatoriamente de todas as possíveis 9 que poderiam ter sido amostradas ao acaso. Por esta razão, praias é um variável aleatória.
O efeito aleatório praia organiza parte da variação nos nossos dados que o modelo não explicaria com as variáveis preditoras e que estaria presente no resíduo($\varepsilon$) do modelo linear simples. Por outro lado, as variáveis preditoras usuais em modelos lineares são chamadas de efeitos fixos. No exemplo das praias, a variável de diferença do nível da maré (NAP) é uma variável de efeito fixo e estamos diretamente interessados em seu efeito sobre a variável resposta (Richness). O nome misto refere-se ao fato de existirem tanto efeitos fixos, quanto aleatórios nas variáveis preditoras do modelo. Esses modelos são chamados também de hierárquicos ou multinível.
Em ecologia é comum encontrarmos delineamentos amostrais ou experimentais que geram dados com algum tipo de agrupamento (delineamento hierárquico ou aninhado). Por exemplo, quando uma amostragem é feita por parcelas ou quando um experimento é separado em diferentes blocos. Nesses casos, não podemos tratar nossos dados como independentes e uma abordagem estatística adequada é a de modelos mistos.
Inicialmente, a forma mais simples de incorporar o efeito aleatório em nosso exemplo é definir que cada praia apresenta um intercepto diferente no modelo. Ou seja, queremos ajustar uma reta para nossa relação entre riqueza e NAP, mas permitir que cada praia tenha seu próprio intercepto, que é relacionado ao intercepto da reta principal (efeito fixo).
Neste caso, o modelo terá a seguinte estrutura:
$$\text{riqueza}_{i} = \alpha + \epsilon_{\text{praia}_i} + \beta * NAP + \epsilon_{\text{res}}$$
sendo:
$$\epsilon_{\text{praia}} = N(0, \sigma_{\text{praia}})$$
$$ \epsilon_{\text{res}} = N(0, \sigma_{\text{res}})$$
A riqueza da praia i é explicada pelo efeito fixo $\beta*NAP$ e pelo efeito aleatório $\epsilon_{\text{praia}_i}$, que se soma ao valor do intercepto fixo do modelo, $\alpha$, para formar o intercepto da praia i. Veja que o índice i está atrelado a $\epsilon_{\text{praia}_i}$ e, portanto, o modelo permite que cada uma das praias apresente um intercepto diferente com mesmas inclinações $\beta$. O $\beta$ faz parte do efeito fixo e não possui nenhum índice i atrelado a ele, portanto, é o mesmo para todas as praias. Finalmente, $\epsilon_{\text{res}}$ representa o resíduo associado aos desvios dos valores observados em relação aos preditos pela reta da praia relativa à observação.
Ambos, $\epsilon_{\text{praia}}$ e $\epsilon_{\text{res}}$, são variáveis aleatórias com média zero e desvios padrão $\sigma_{\text{praia}}$ e $\sigma_{\text{res}}$, respectivamente.
LMM: riqueza em praias
Lendo os dados praias no R
- baixe o arquivo vamos à praia;
- no Rcmdr, importe o arquivo, que está formatado com campos separados por tabulação e decimal como ponto;
- atribua o nome de
praiaao conjunto de dados; - visualize o conjunto de dados para se familiarizar com as variáveis.
Um modelo plausível: riqueza em praias
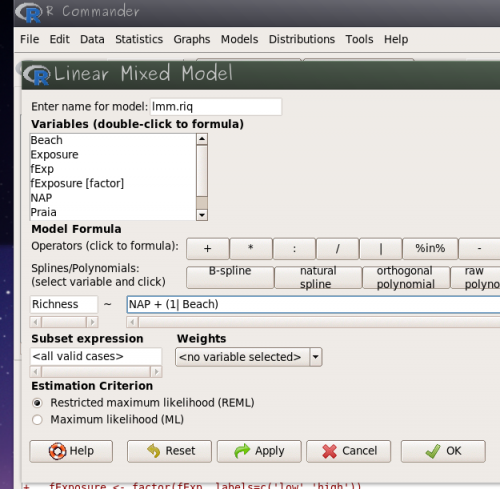
Vamos construir um modelo simmples que tem apenas NAP como variável fixa preditora e a variável Beach como aleatória apenas no intercepto. Esse modelo pode ser descrito no lme4 da seguinte forma10):
Richness ~ NAP + (1 | Beach)
No Rcmdr siga os passos:
- abra o menu
Statistics>Fit models>Linear mixed models… - nomeie o modelo como
lmm.riqe coloque a fórmula acima nos campos adequados
Em seguida, vamos dar uma olhada no resultado deste modelo que aparece na janela inferior do Rcmdr.
Interpretando o modelo: riqueza em praias
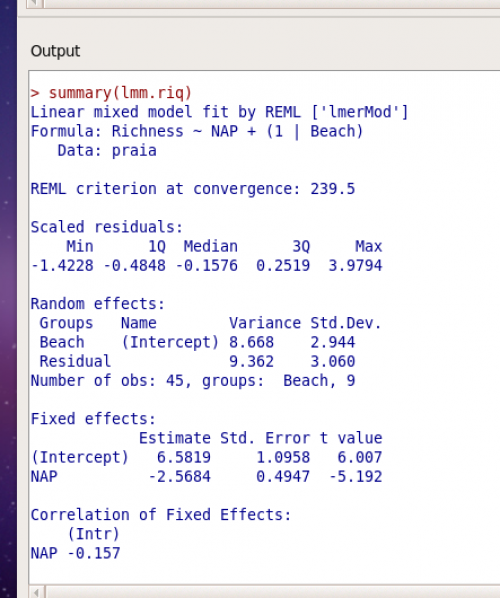
Na figura abaixo temos o resultado resumido do modelo lmm.riq:
Vamos começar olhando a parte dos efeitos aleatórios (Random effects). O desvio padrão (Std.Dev.) é uma medida do quanto a variabilidade da nossa variável dependente Richness é particionada aos efeitos aleatórios que estamos analisando (Beach) e o quanto não foi explicado (Residual). Podemos ver em Beach o desvio padrão associado às diferenças de intercepto entre praias ( $\sigma_{\text{praia}}$ do modelo associado ao $\epsilon_{\text{praia}}$). A última linha apresenta o resíduo, que indica o quanto da variabilidade não é prevista pela variável aleatória praia nem pela variável fixa NAP, ou seja, o que não é explicado por nenhum termo do nosso modelo.
Na seção Fixed effects são apresentados os coeficientes estimados para cada um dos fatores que estamos considerando como fixos. No caso, temos o intercepto médio11) associado à riqueza quando o NAP é zero (6.5819) e o coeficiente angular de NAP (-2.5684), que indica que há uma diminuição de riqueza da ordem de mais de 2.5 espécies a cada unidade de NAP acrescida.
Note que nesse modelo a inclinação é a mesma para todas as praias e que o intercepto da estrutura fixa é o intercepto médio dos coeficientes da estrutura aleatória do modelo.
A correlação dos efeitos fixos é o quanto os coeficientes fixos estimados são correlacionados. Mais formalmente é uma estimativa do quanto teríamos de correlação entre o intercepto e a inclinação se refizessemos o experimento muitas vezes12). Apesar de ser apresentada por padrão no resumo do lme4 essas correlações não tem uma interpretação direta e muito menos intuitiva 13).
Predito pelo Modelo: riqueza em praias
Uma boa maneira de interpretar os resultados é a partir do gráfico do predito pelo modelo, se possível junto aos valores das observações dos dados. Temos apresentado gráficos com a experança do modelo ao longo de todo o curso na intenção de auxiliar na interpretação do modelo. Além disso, calcular o predito através dos coeficientes do modelo ajuda a entender a estrutura atrás dos coeficientes.
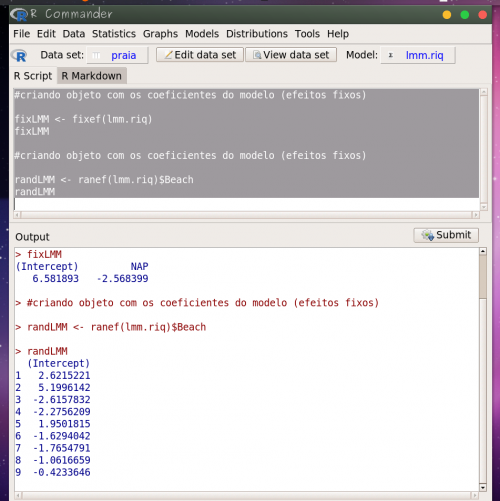
Para fazer o gráfico do modelo ajustado, com a reta média predita pela estrutura fixa do modelo e as retas da estrutura aleatória, preditas para cada praia, vamos criar um objeto no Rcmdr com todos os coeficientes necessários. Copie as linhas de código a seguir no painel superior do Rcmdr (o painel chamado Rscript), em seguida, selecione todas as linhas copiadas e clique no botão Submit 14).
#criando objeto com os coeficientes do modelo (efeitos fixos) fixLMM <- fixef(lmm.riq) fixLMM #criando objeto com os coeficientes do modelo (efeitos aleatorios) randLMM <- ranef(lmm.riq)$Beach randLMM
O predito pela estrutura das variáveis fixas do modelo estimam o modelo médio, que seria a esperança do modelo para uma praia média, ponderada pelas observações de cada uma das praias. Além disso, a estrutura aleatória do modelo prediz um intercepto para cada praia das nossas observações a partir da variabiabilidade existente entre praias, definido pelo efeito aleatório $\epsilon_{praia}$.
Note que nesse modelo temos apenas um coeficiente de inclinação, pois não modelamos a inclinação na estrutura aleatória do modelo, apenas o intercepto. Mais adiante faremos um modelo incluindo inclinação para a variável aleatória e poderemos comparar os resultados.
Gráfico do Modelo: riqueza em praias
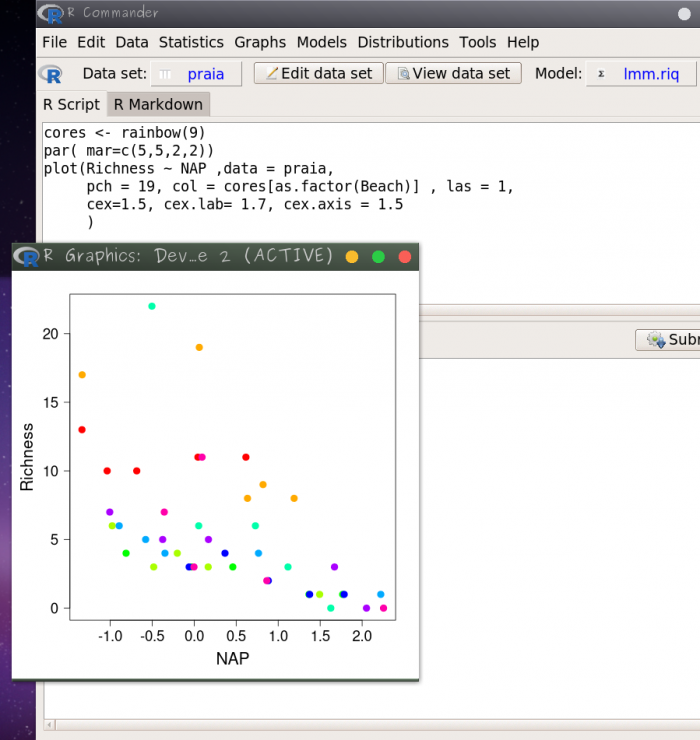
Vamos primeiro construir um gráfico base, com os valores observados. Para tornar o gráfico mais informativo vamos colocar cores para identificar em que praia cada observação foi coletada. No código abaixo temos as seguintes sequência de eventos:
cores…: cria um objeto com nove cores tiradas de uma paleta das cores do arco-írispar(…): modifica parâmetros da janela gráfica, no caso abaixo modificamos as margens do gráficoplot(…): cria o gráfico- 1° linha: indica quais variáveis devem estar no eixo Y e X, e em qual objeto estão os dados
- 2° e 3° linhas: modificações de parâmetros do gráfico, como símbolos, letras, etc
Então, copie os códigos abaixo para a janela superior do Rcmdr (RScript), selecione essas linhas e aperte o botão Submit:
cores <- rainbow(9)
par( mar=c(5,5,2,2))
plot(Richness ~ NAP ,data = praia,
pch = 19, col = cores[as.factor(Beach)] , las = 1,
cex=1.5, cex.lab= 1.7, cex.axis = 1.5
)
Incluindo o modelo no gráfico
Vamos usar os valores dos coeficientes (aqueles que calculamos anteriormente com as funções fixef e ranef) para representar as esperanças do modelo e criar as retas para cada praia e a reta média.
Primeiro o gráfico com as retas de cada praia:
Copie os códigos abaixo para a janela superior do Rcmdr (RScript), selecione essas linhas e aperte o botão Submit:
abline(randLMM[1,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[1]) abline(randLMM[2,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[2]) abline(randLMM[3,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[3]) abline(randLMM[4,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[4]) abline(randLMM[5,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[5]) abline(randLMM[6,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[6]) abline(randLMM[7,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[7]) abline(randLMM[8,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[8]) abline(randLMM[9,'(Intercept)']+ fixLMM[1], fixLMM[2], col=cores[9])
Para finalizar o gráfico, vamos colocar o predito pelo modelo médio e uma legenda:
Repita o mesmo procedimento de copiar, selecionar e “submeter”:
abline(fixLMM[1], fixLMM[2], col = "black", lwd=3, lty= 2)
legend("topright", c( "praia média",paste("praia", 1:9)) , lty=c(2, rep(1,9)), col= c(1,cores), bty="n", cex=1.2)
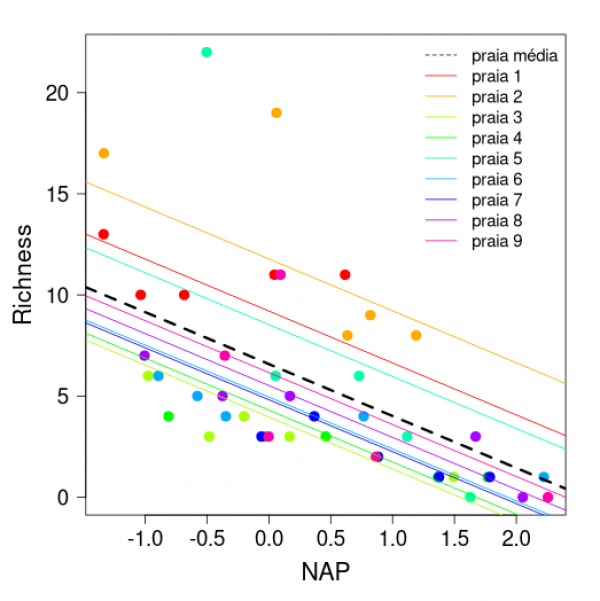
Ao final o nosso gráfico deve ser parecido com o que está a seguir:
Podemos ver nessa figura a predição do nosso modelo em relação aos parâmetros fixos (reta tracejada em preto) e as predições para cada praia separadamente. Como o efeito aleatório do nosso modelo estava apenas variando os valores de intercepto das praias, as retas para cada praia são paralelas.
Seleção de LMM: riqueza em praias
Uma questão central em planejamento e análise de dados é decidir como compor um conjunto de modelos plausíveis a partir das hipóteses e um conjunto de variáveis. Além disso, a partir deste conjunto de modelos plausíveis, é preciso tomar a decisão sobre qual15) é o melhor para representar nossos dados. Nesse curso utilizamos a partição da variação para comparar modelos aninhados. Vamos continuar a usar o mesmo procedimento, ou seja, fazer o teste de hipótese para comparar modelos dois a dois a partir do modelo cheio para chegar ao mínimo adequado. Esse procedimento se torna mais complexo nos modelos mistos ao envolver a simplificação da estrutura aleatória, além da estrutura fixa, como fizemos nos modelos anteriores.
Existem diversas possibilidades de modelos com esses mesmos dados. Por exemplo, podemos adicionar o nível de exposição de cada praia (Exposure) como uma variável preditora fixa categórica e/ou podemos inserir o efeito aleatório da variável Beach na inclinação da variável NAP (efeito fixo). Essa inclusão da interação entre a variável aleatória (Beach) e a preditora fixa contínua (NAP) faz com que cada praia possa também ter uma relação específica com NAP (inclinações de reta diferentes para cada praia), mas sempre ponderadas pela relação média.
Ajustando os dados: riqueza em praias
Os dados que estamos usando estão disponíveis no github do livro do Zuur et al. (2009). A variável Exposure originalmente tem 3 níveis: 8, 10 e 11. Como o nível 8 foi observado apenas em uma praia, reclassificamos esta praia para o nível seguinte, no caso o 10 (Zuur et al. 2009).
A partir da variável Exposure, criamos a fExp que contempla apenas os valores 10 e 11 para designar os dois níveis de exposição das praias. Para tornar essa variável mais explicita com relação ao seu significado vamos transformar os valores 10 e 11 de fExp em fatores low e high, nesta ordem, criando uma nova variável fExposure:
- abra o menu
Data>Manage variables in active data set>Convert numeric variables to factors…; - coloque o nome da nova variável como
fExposureno campo<same as variable>; - deixe selecionada a opção
Supply level names; - no quadro que irá se abrir digite
lowpara o valor10ehighpara o valor11; - após criar verifique se a variável foi corretamente criada clicando no botão
View data set.
Seleção dos efeitos aleatórios: riqueza em praias
Existem modelos e, portanto, perguntas e delineamentos amostrais que requerem apenas um efeito aleatório para indicar o agrupamento dos dados. Entretanto, como colocado na seção anterior, há também modelos que podem incluir mais de um efeito aleatório. Esse é o caso da interação entre praia e NAP mencionada acima.
Para conjunto de modelos plausíveis com diferentes efeito aleatório, Zuur et al. (2009) sugerem um protocolo para a escolha da melhor estrutura de efeitos aleatórios, que vamos seguir neste curso. Os passos principais deste procedimento são listados a seguir.
I. Incluir no modelo cheio todos os efeitos fixos de interesse, incluindo termos de interação e qualquer ou estrutura não aleatória, no caso teremos os efeitos fixos:
Richness ~ fExposure + NAP + fExposure:NAP
II. associar a esta estrutura fixa cheia os efeitos aleatórios plausíveis em sua estrutura mais complexa. No nosso exemplo, temos duas possibilidades de efeito aleatório:
- apenas variações no intercepto entre praias (
(1|Beach)); - contendo a interação entre praia e NAP, resultando também na variação de inclinação entre praias (
(NAP|Beach));
Os modelos mistos serão ajustados utilizando uma forma diferente de estimar os parâmetros. Ao invés da máxima verossimilhança (ML - Maximum Likelihood) que utilizamos nos modelos lineares os modelos mistos usam a máxima verossimilhança restrita (REML - Restricted Maximum Likelihood). Isso acontece porque a ML é enviesada para as estimativas de variância e a REML corrige esse viés. Na prática, nós não precisamos fazer nada, pois a função lmer do pacote lme4utiliza a REML (argumento REML = TRUE) como padrão.
III. utilizar anova para comparar modelos com estruturas aleatórias aninhadas e mesma estrutura fixa cheia, buscando a simplificação da estrutura aleatória. Para que a comparação seja feita com o REML é preciso usar o argumento da função anova como refit = FALSE;
IV. Mantenha a estrutura aleatória selecionada e siga simplificando a estrutura fixa, comparando modelos aninhados por anova. Utilize o padrão da anova com o argumento refit = TRUE.
Poderíamos também ajustar um modelo sem efeito aleatório (usando a função lm) e ver se a inclusão do efeito aleatório resulta em um melhor ajuste do modelo, entretanto, a dependência entre as amostras de uma mesma praia são parte do desenho experimental dos dados e acreditamos que essa característica deve ser mantida no modelo. Além disso, é importante lembrar que a retirada de todos os efeitos aleatórios superestima os graus de liberdade do modelo, ou seja o modelo linear estaria inflado no seu poder de explicação da variabilidade dos dados.
A sequência do procedimento de simplificação da estrutura aleatória para o nosso exemplo, seria:
- Criar o modelo
lmmfullcom todos os efeitos aleatórios, pelo menu do RcmdrStatistic>Linear mixed models…deixando o argumento com o padrãoREML=TRUEe inserindo os termos do modelo como indicado abaixo:
Richness ~ fExposure + NAP + fExposure:NAP + (NAP|Beach)
- Em seguida faça o mesmo procedimento para criar o modelo
lmmintcom a variável aleatória somente no intercepto:
Richness ~ fExposure + NAP + fExposure:NAP + (1|Beach)
- Compare os modelos anteriores com o comando
anovabuscando a simplificação do modelo ao mínimo adequado16), usando o menu do RcmdrModels > Hipothesis tests > Compare two models…e selecionando os modeloslmmintelmmfull.
Um problema com a interface do Rcmdr é que precisamos incluir o argumento refit = FALSE na função anova para garantir que o procedimento irá manter a estimativa por REML e não irá reajustar os modelos por ML antes de comparar os modelos. O padrão da função anova quando aplicada à comparação de dois modelos mistos é reajustar para ML. Como a interface não oferece essa opção precisamos editar a linha de comando do painel superior.
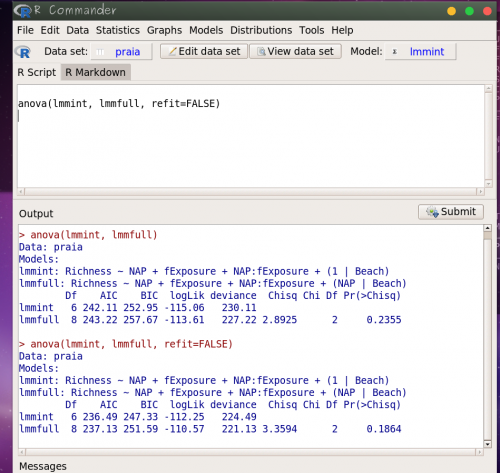
Quando você clicou ok na função anova de comparação de modelos, apareceu esse código na janela superior do Rcmdr:
anova(lmmint, lmmfull)
copie esse código novamente no painel superior, mas agora inclua a expressão refit = FALSE, como indicado abaixo:
anova(lmmint, lmmfull, refit= FALSE)
Selecione essa linha e clique no botão Submit. O resultado deve ser como o apresentado abaixo:
Note que as estimativas do primeiro resultado (ou seja, da anova com reajuste para ML) e do segundo resultado (ou seja, sem reajuste para ML, usando refit = FALSE) são diferentes. É importante saber que no processo de simplificação da estrutura aleatória do modelo devemos ignorar os primeiros resultados, pois não queremos que seja feito um reajuste para ML, ou seja, queremos que a comparação das estruturas aleatórias seja feita usando as estimativas por REML.
O “p-valor” observado nessa comparação é alto, indicando que os modelos não apresentam diferenças marcantes, sendo assim, devemos reter o modelo mais simples e seguimos simplificando. Como só há mais um termo na estrutura aleatória modelando o intercepto, podemos finalizar a seleção da estrutura aleatória aqui.
Alguns autores 17) advogam que se nenhum termo da estrutura aleatória for significativo, deve-se abandonar o modelo misto e partir para o modelo linear sem estrutura aleatória. De fato, isso facilitaria muito a interpretação e a apresentação dos resultados do modelo. Porém, outros autores que seguiremos aqui, indicam que devemos manter a coerência do delineamento experimental/amostral e portanto devemos contemplar a dependência das observações de uma mesma praia, utilizando o modelo com a variável aleatória Beach no intercepto.
Após simplificar a estrutura de efeito aleatório o resultado é que as praias diferem na riqueza média, mas essa variação das praias não influencia a relação de Richness com o NAP.
Note que quando observamos o primeiro gráfico desse tutorial, parecia que a inclusão de diferentes inclinações para cada praia no modelo seria importante. Porém, o resultado desse teste acima nos indica que, apesar de algumas praias terem inclinações aparentemente diferentes, não ganhamos muita informação adicional relevante ao incluir inclinações diferentes para todas as nove praias.
Estrutura fixa do modelo: riqueza de praias
O próximo passo é prosseguir com a verificação e simplificação dos efeitos fixos através do mesmo método que utilizamos até então. Relembrando, estamos interessados em verificar se existe um efeito de NAP, fExposure e da interação NAP:fExposure na riqueza de espécies. Começamos com o nosso modelo com todos os efeitos fixos e a estrutura aleatória já simplificada:
Richness ~ fExposure + NAP + fExposure:NAP + (1|Beach)
Primeiro iremos simplificar retirando o termo fixo mais complexo, a interação fExposure:NAP:
Richness ~ fExposure + NAP + (1 | Beach)
Caso o modelo mais simples tenha um poder de explicação da variação dos dados similar ao mais complexo, devemos continuar a simplificação com os modelos só com NAP ou só com fExposure. Nos dois casos iremos comparar com o modelo que contém ambos termos fExposure + NAP, para que os modelos comparados sejam aninhados 18).
Siga a simplificação até chegar ao modelo mínimo adequado para esse conjunto de dados.
Diagnósticos dos modelos
Depois de selecionado o modelo que melhor se ajusta aos nossos dados é sempre necessário avaliar o ajuste deste modelo a suas premissas. O Rcmdr faz alguns gráficos diagnósticos e de efeito do modelo que podem ser explorados no menu: Models > Graph.
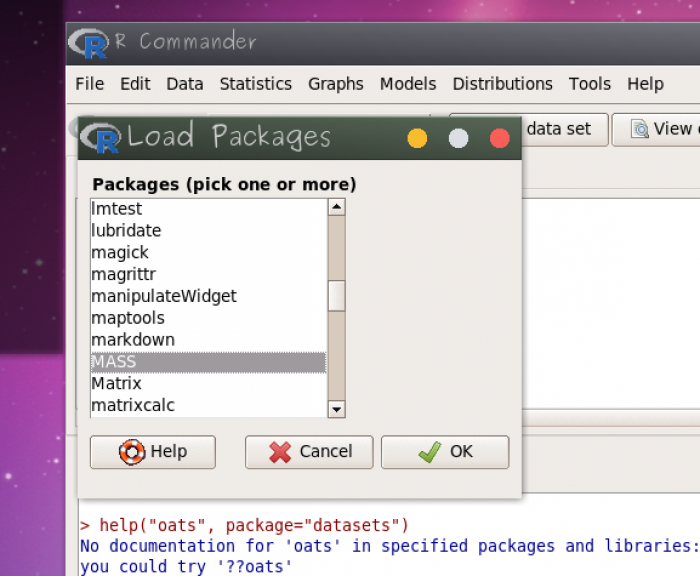
Para a construção de outros gráficos diagnósticos podemos carregar o pacote lattice, selecionando-o pelo menu Tools > Load package(s)….
Depois, copie os códigos abaixo no painel superior (RScript) do Rcmdr, mas, antes de apertar o botão Submit substitua o argumento NOME_DO_MODELO pelo nome do seu modelo mínimo adequado19). Depois disso pode selecionar e submeter as linhas de comando.
Atenção: Faça um gráfico de cada vez e salve o pdf de cada gráfico antes de começar a fazer o próximo
## 1) gráfico quantil-quantil (normalidade) qqmath(NOME_DO_MODELO,id=0.05)
## 2) gráfico de valores ajustados x resíduos (homocedasticidade)
plot(NOME_DO_MODELO,type=c("p","smooth"))
## 3) gráfico de valores ajustados x resíduos padronizados (homocedasticidade)
plot(NOME_DO_MODELO,sqrt(abs(resid(.)))~fitted(.), type=c("p","smooth"))
OPS! Olhando o gráfico diagnóstico dos resíduos, parece que os dados não são tão homocedásticos como deveriam, pois vemos algo parecido com um funil se abrindo da esquerda para a direita, o que indica que o modelo viola esta premissa. Isso não deveria ser um
Ajustando os dados
Os dados que estamos usando estão disponíveis no github do livro do Zuur et al. (2009). A variável Exposure originalmente tem 3 níveis: 8, 10 e 11. Como o nível 8 foi observado apenas em uma praia, reclassificamos esta praia para o nível seguinte, no caso o 10 (Zuur et al. 2009).
A partir da variável Exposure, criamos a fExp que contempla apenas os valores 10 e 11 para designar os dois níveis de exposição das praias. Para tornar essa variável mais explicita com relação ao seu significado vamos transformar os valores 10 e 11 de fExp em fatores low e high, nesta ordem, criando uma nova variável fExposure:
- abra o menu
Data>Manage variables in active data set>Convert numeric variables to factors…; - coloque o nome da nova variável como
fExposureno campo<same as variable>; - deixe selecionada a opção
Supply level names; - no quadro que irá se abrir digite
lowpara o valor10ehighpara o valor11; - após criar verifique se a variável foi corretamente criada clicando no botão
View data set.
a surpresa já que a variável Richness é uma contagem e como tal tem a variância acoplada à média.
E agora??! Bem, quase sempre existe um caminho! O problema aqui é que assumimos que a riqueza de espécies, uma variável de contagem, poderia ser modelada como uma distribuição normal. Entretanto, dados de contagem geralmente são melhor modelados usando a distribuição de Poisson. Já aprendemos isso no tutorial Modelos Lineares Generalizados: contagem.
Então, para fazermos a modelagem correta dos nossos dados teremos que usar um modelo com distribuição de Poisson dentro do contexto de modelo misto. Nesse caso teríamos que usar uma classe de modelos que junta o GLM com o LMM que se chama Modelo Generalizado Misto.
Mas isso é tema para outro roteiro… Modelos Generalizados Mistos (GLMM)
PARA ENTREGAR ANTES DA PRÓXIMA AULA Acesse o formulário e responda às questões propostas referentes aos dados sobre a riqueza em praias.
Cultivando aveia
Nesse experimento clássico descrito por Yates em 1935, foram utilizadas três variedades de aveia tratadas com 4 níveis de adubação com nitrogênio. O desenho experimental deste estudo20) é bastante complexo e contempla diferentes níveis de dependência das observações que precisam ser incorporadas no modelo como variáveis aleatórias. Vamos entender esse estudo.
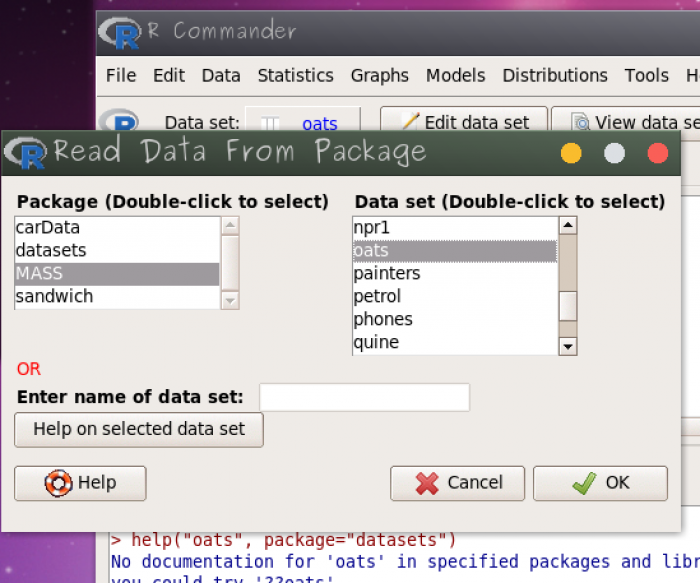
O primeiro passo é fazer a leitura dos dados do objeto oats que se encontra no pacote MASS:
Entendendo Aveia
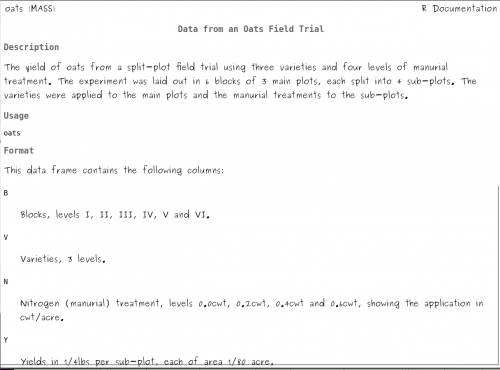
Para entender os dados utilize o menu Help > Help on active data set (if available) e leia a documentação que irá se abrir onde há uma descrição das variáveis:
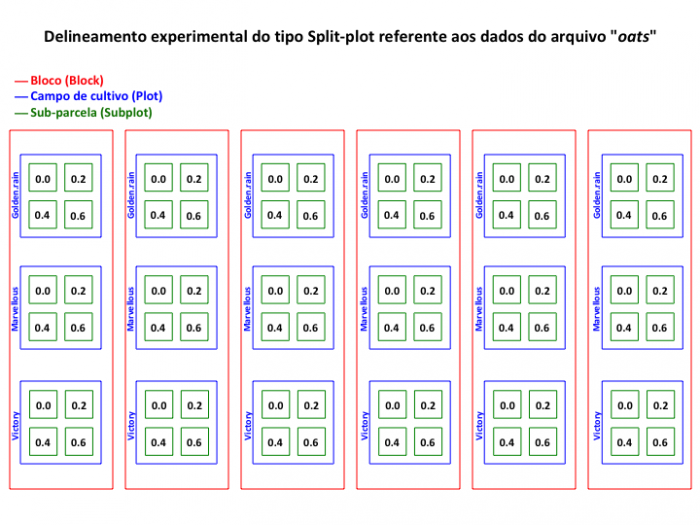
O desenho experimental contempla 6 localidades (B de Blocks) distintas, sendo que cada uma apresenta três campos de cultivo (plot) para cada variedade de aveia (V de Varieties). Cada campo, por sua vez, é dividido em quatro partes (subplot) com os diferentes tratamentos com adubo nitrogenado (N de Nitrogen treatment). No desenho experimental temos um aninhamento de bloco com plot e subplot. Para auxiliar no entendimento deste desenho experimental, preparamos a figura abaixo:
Ajustando os dados de Aveia
As variáveis plot e subplot não estão nesse conjunto de dados, mas podem ser resgatadas pelo fato de plot ser o campo onde foi cultivada cada variedade. Só precisaremos criar a variável plot, pois a subdivisão dos campos de cultivo nos diferentes níveis de adubação (que seriam os subplots) não precisa ser indicada no modelo, uma vez que essa divisão representa o menor nível hierárquico e a função lmer já reconhece esse nível automaticamente.
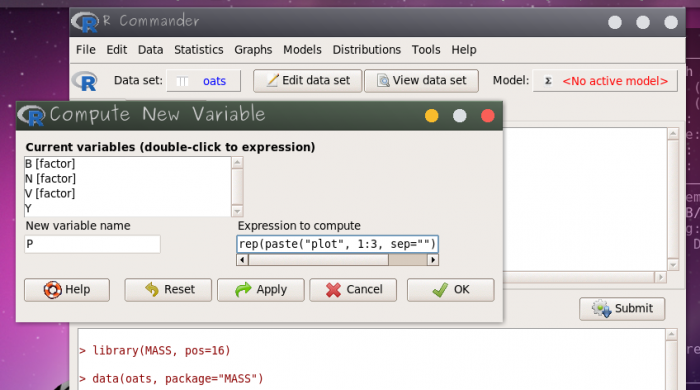
Para criar plot vamos usar o menu Data > Manage variable in active data set > Compute new variable e utilize o nome P (plot) no campo New variable name e no campo Expression to compute insira o código abaixo:
rep(paste("plot", 1:3, sep=""), each=4)
Esse código irá criar uma nova variável P com os níveis plot1, plot2 e plot3 para cada campo de cultivo de cada variedade de aveia, nos quais os níveis de adubação estão incluídos (4 níveis). Apesar da variável P estar no mesmo nível da variável V, fazemos isso para explicitar que P é diferente de V, sendo que uma representa os campos de cultivo e a outra representa as variedades de aveia cultivadas, respectivamente. Note também que os códigos de P se repetem entre os blocos, apesar de serem unidades distintas, ou seja, o campo de cultivo plot1 do bloco I é outro campo de cultivo do que o plot1 do bloco II. Por outro lado, as variedades se repetem entre os blocos, ou seja, a variedade Marvellous é Marvellous em qualquer bloco.
Atividade
- Construa um modelo cheio tendo como variável resposta o rendimento de cultivo (
Y) e como preditoras as variáveis fixas variedade (V), adubação nitrogenada (N) e a interação entre as duas. Como estrutura aleatória utilize o fator aleatório plot (P) aninhado dentro de bloco (B), com a sintaxe(1|B/P). Note que, como não temos variáveis fixas contínuas, apenas categóricas, não há como modelar a inclinação do modelo, apenas o intercepto. - Faça a simplificação da estrutura fixa das preditoras e chegue ao modelo mínimo adequado.
- Faça a interpretação biológica do resultado baseado nos coeficientes fixos e da variação associada aos fatores aleatórios.
Se você se interessou pelos modelos mistos e acha que eles se encaixam no seu problema, não deixe de conferir as referências listadas abaixo para se aprofundar. Os modelos mistos são muito flexíveis e uma ferramenta poderosa para comtemplar muitas das dependencias que temos em desenhos experimentais na biologia.
Exercício
PARA ENTREGAR ANTES DA PRÓXIMA AULA Acesse o formulário e responda às questões propostas referentes aos dois exemplos (Praias e Aveia) trabalhados nesse tutorial.
Referências e recomendações
Bates, et al. 2014.Fitting linear mixed-effects models using lme4. arXiv preprint arXiv:1406.5823. (publicação do pacote `lme4`)
Burnham, K. & Anderson, D. 2002. Model selection and multimodel inference: a practical information-theoretic approach. 2nd edn. New York: Springer-Verlag. (Livro sobre a abordagem de seleção de modelos baseada em Teoria da Informação)
McGill, B. 2015. Is it a fixed or random effect? Blog Dynamic Ecology. (Uma boa discussão sobre o que são efeitos fixos e aleatórios)
Winter, B. 2013. Linear models and linear mixed effects models in R with linguistic applications. arXiv:1308.5499. (Nesse excelente roteiro, o autor explica modelos lineares e depois apresenta modelos mistos de uma forma bem didática)
Yates, F. 1935. Complex experiments. Journal of the Royal Statistical Society Suppl. 2, 181-247. (O experimento de aveia que tratamos nesse roteiro é descrito nesse artigo).
Zuur, A., Ieno, E., Walker, N., Saveliev, A. & Smith, G. 2009. Mixed effects models and extensions in ecology with R. (Livro muito bom e completo sobre modelos mistos e aditivos)
R diretamente, você precisará instalar e carregar o mesmo pacote15.7%. Essa correlação é calculada à partir da matriz de variância/covariância do modelo e pode ser calculada para qualquer modelo com estrutura fixa. Uma confusão comum é achar que esse valor está associada necessariamente à multicolinearidade das variáveis preditoras, o que não é o caso.correlation = FALSE na função summary# não são lidas pelo Rcmdr e podem ser usadas para comentar as linhas de código, isso ajuda a lembrar o que a linha de código fazNAP incorpora o intercepto também, apesar de não estar explicito na nossa formulaçãoNAP com o modelo só com fExposure!Rcmdr designou ao modelosplit-plot