Ferramentas do usuário
−Barra lateral
−Tabela de conteúdos
Modelos Lineares Generalizados: contagem
GLM: introdução
Essa introdução aos GLM é a mesma do tutorial Modelos Lineares Generalizados: binomial, caso já tenha feito, pode passar diretamente para o tópico GLM: contagem
Os modelos lineares generalizados (GLMs) são uma ampliação dos modelos lineares ordinários. Os GLM's são usados quando os resíduos (erro) do modelo apresentam distribuição diferente da normal (gaussiana). A natureza da variável resposta é uma boa indicação do tipo de distribuição de resíduos que iremos encontrar nos modelos. Por exemplos, variáveis de contagem são inteiras e apresentam os valores limitados no zero. Esse tipo de variável, em geral, tem uma distribuição de erros assimétrica para valores baixos e uma variância que aumenta com a média dos valores preditos, violando duas premissas dos modelos lineares. Os casos mais comuns de modelos generalizados são de variáveis resposta de contagem, proporção e binária, muito comum nos estudos de ecologia e evolução.
Devemos considerar os GLMs principalmente quando a variável resposta é expressa em:
- contagens simples
- contagem expressa em proporções
- número de sucesso e tentativa
- variáveis binárias (ex. morto x vivo)
- tempo para o evento ocorrer (modelos de sobrevivência)
GLM: componentes
Uma das formas de entendermos os modelos generalizados é separar o modelo em dois componentes: a relação determinística entre as variáveis (resposta e preditora) e o componente aleatório dos resíduos (distribuição dos erros). Em um modelo linear ordinário a relação entre as variáveis é uma proporção constante, o que define uma relação funcional de uma reta. Quando temos uma contagem, essa relação pode ter uma estrutura funcional de uma exponencial. Para esses casos, os modelos generalizados utilizam uma função de ligação log para linearizar a relação determinística entre as variáveis. Portanto, a estrutura determinística dos modelos GLM's é definida por um preditor linear, associada à função de ligação.
O componente aleatório dos resíduos, no caso de uma variável de contagem, segue, em geral, uma distribuição poisson. A distribuição poisson é uma variável aleatória definida por apenas um parâmetro (λ), equivalente à média, chamada de lambda. A distribuição poisson tem uma característica interessante, seu desvio padrão é igual à média. Portanto, se a média aumenta, o desvio acompanha esse aumento e a distribuição passa a ter um maior espalhamento.
Preditor linear e função de ligação
O preditor linear está associado à estrutura determinística do modelo e está relacionado à linearização da relação, aqui definido como η:
η=α+βx
A função de ligação é o que relaciona o preditor linear com a esperança do modelo:
η=g−1(E(y))
Ou seja, nos modelos generalizados não é a variável resposta que tem uma relação linear com a preditora, e sim o preditor linear que tem uma relação linear com as preditoras.
Funções de ligações canônicas
Para alguns tipos de famílias de variáveis temos funções de ligações padrões. As mais usadas são:
| Natureza da resposta | Estrutura dos resíduos (erro) | Função de ligação |
|---|---|---|
| contínua | normal | identidade |
| contagem | poisson | log |
| proporção | binomial | logit |
GLM: dispersão e acumulo de zeros
Os modelo GLM poisson e binomial apresentam a variância acoplada à média dos valores, diferentemente dos modelos com distribuição normal onde a média e a variância são independentes. Caso haja uma variação maior ou menor nos dados do que o previsto por essas distribuições, o modelo não consegue dar conta. Essa sobre-dispersão ou sub-dispersão dos dados indica que temos mais ou menos variação do que é predito pelos modelos. Isso pode ser decorrência de vários fontes de erro na definição do modelo, alguns exemplos são:
- o resíduo dos dados pode não ter sido gerado por um processo aleatório poisson ou binomial
- há mais variação do que predito pela ausência de preditoras importantes
- muitos zeros, além do predito pelas distribuições, em decorrência de diferentes processos: um que gera a ausência e outro que gera a variação nas ocorrências de sucesso
Soluções para a sobre-dispersão e acumulo de zeros
A solução mais simples para lidar com a dispersão são os modelo quasipoisson e quasibinomial, que estimam um parâmetro a mais, relacionando a média à variância, o parâmetro de dispersão. Entretanto, os modelos quasi dão conta apenas de dispersões moderadas e não indicam qual a fonte dela.
Há algumas alternativas ao modelo quasi para a dispersão dos dados, alguns deles estão listados abaixo:
- modelo binomial negativo
- modelo de mistura, considerando dois processos distintos
- modelos mistos, considerando a ausência de independência das observações
- modelos com acúmulos de zeros (Zero Inflated Models).
Não é objetivo deste curso mostrar todas essas alternativas, mas caso se deparem com esse problema, muito frequente na área da biológica, saibam que existem alternativas robustas para solucioná-lo.
Variável resposta binária é um caso especial da binomial com apenas uma tentativa, chamado de distribuição de Bernoulli, e não tem problema com sobre-dispersão
GLM: contagem
Contagem: um exemplo simples
Um exemplo, apresentado no livro do Michael Crawley, The R Book, relata a contagem de espécies de árvores em unidades amostrais de florestas com diferentes biomassa e classificadas em três níveis de ph no solo: baixo, médio e alto. O objetivo desse experimento não manipulativo é verificar se há relação entre riqueza de árvores e as preditora biomassa da floresta e ph do solo.
ATIVIDADE
Modelo Linear Múltiplo (LM)
- Importe o arquivo species.txt para o Rcmdr. Note que esse arquivo tem como separador de campo a tabulação e decimal como ponto.
- Monte o modelo linear clássicos (
lm) para esse dados, tendo como variável resposta a riqueza de espécies(Species) e como preditoras opHeBiomasse as interações possíveis. - Reduza o modelo cheio ao modelo mínimo adequado utilizando como critério de comparação a tabela de anova.
- Utilizando os coeficientes estimados do modelo, faça a predição do número de espécies para:
- um nível alto de
pHcomBiomassde 3.2 - um nível médio de
pHcomBiomassde 15.5 - um nível baixo de
pHcomBiomassde 7.1
Modelo Linear Generalizado (GLM)
- Repita o procedimento de simplificação a partir do modelo cheio, agora com modelo linear generalizado (
glm) e comfamily = poisson.- Caso o Rcmdr não retorne o
p-valorna comparação de modelos por anova, copie a linha de código que foi utilizada comanova(…)e cole novamente incluindoanova(…, test=“Chisq”)
- Calcule as mesmas predições acima para o modelo, usando os coeficientes do preditor linear do
glm. - Transforme os preditos pelo modelo de volta para a escala de observação 1).
- Faça os gráficos apresentados no tópico Gráfico no Rcmdr
- Para a predição no
glmutilize os coeficientes estimados pelo modelo. - Após estimar o predito na escala linear, transforme a predição para a escala de observação.
- Como usamos o
logcomo função de ligação, para retornar a escala da observação devemos utilizar o antilog, no caso, a função exponencial.
Gráfico no Rcmdr
Gráfico dos dados
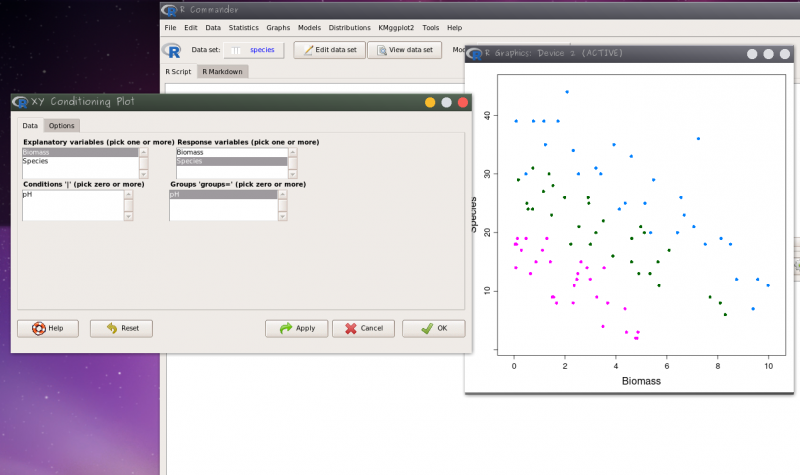
No menu Graphs, selecione XY conditioningh Plot e selecione as varíáveis, definindo ph como variável de agrupamento, como no gráfico abaixo.
Gráfico dos Modelos
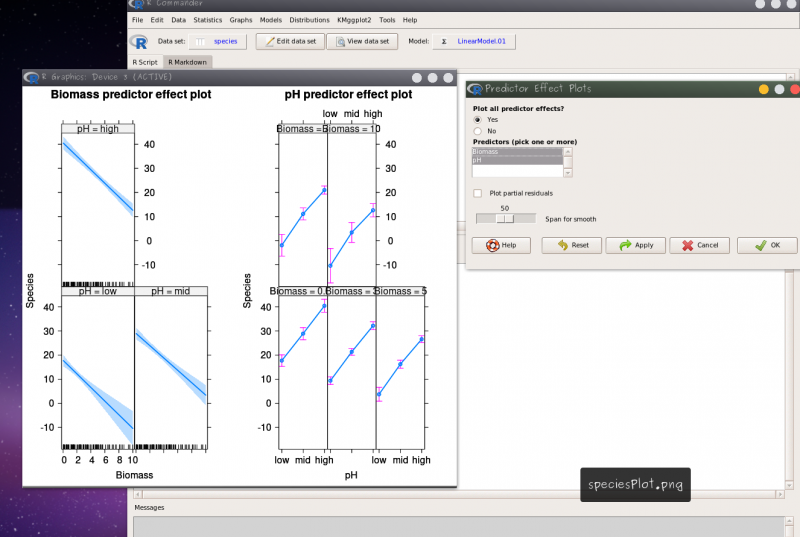
No menu Models>Graphs selecione Predict effect plots… e selecione as variáveis.
Ordenando uma categórica
O padrão do R é ordenar as variáveis categóricas por ordem alfabética. No exemplo seria desejável reordenar a variável categórica ph em uma categórica ordenada low>medium>high.
- reordene a variável
phutilizando o menuData>Manager variable in active data set> Reorder factor levels - crie a variável
factorcom o nomephFna caixafactor namee selecion a caixaFaça fator ordenado, em seguida clique emOK; - reordene as variáveis inserindo
1,2e3nas caixas dos níveislow,medium,high
Formulário de Perguntas
- Responda as perguntas do formulário
Contagem: o que faz um aluno faltar às aulas
Vamos utilizar um exemplo que está presente no livro de W. Venables e B. Ripley, Modern Applied Statistics with S-PLUS2), sobre o número de dias ausentes da escola de crianças na Austrália.
Carregando o pacote MASS
No Rcommader (Rcmdr) vá ao menu Tools > Load package(s) e selecione o pacote MASS.
Caso o pacote não apareça listado, significa que ele já está carregado, então pule esse passo.
Lendo os dados: quine
Em sequida:
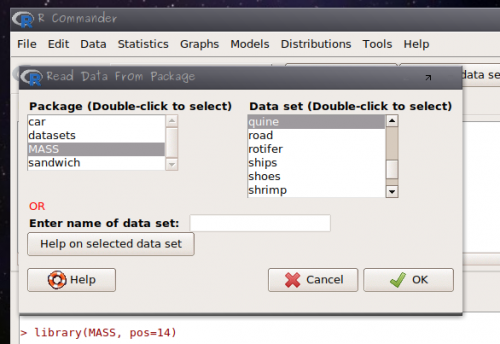
- abra o menu Data > Data in packages > Read data from an attached package…
- selecione o pacote MASS e os dados quine 3)
Entendendo os dados: quine
Os dados estão relacionados ao estudo para entender quais variáveis estão relacionados à ausência (falta) do aluno na escola. A observação está relacionada a alunos amostrados aleatoriamente de escolas na Austrália.
- Days: variável resposta, número de dias ausente da escola
- Eth: origem aborígene (A) ou não (N)
- Sex: homem (M) ou mulher (F)
- Age: estágio de educação F0(primário)… quatro níveis.
- Lrn: classificação de aprendizado do aluno médio (AL) e fraco (SL)4)
Gráfico dos dados
O pacote RcmdrPlugin.KMggplot2 é um plugin para Rcmdr que amplia as funções gráficas da interface. Instale o pacote copiando o comando abaixo no box superior do Rcmdr:
- guarde os resultados dos modelos fora do Rcmdr pois a instalação e o carregamento do pacote solicita a reinicialização do Rcmdr
- após a instalação e carregamento do pacote, confira se os dados permanecem ativos, confira se precisará carregá-lo novamente
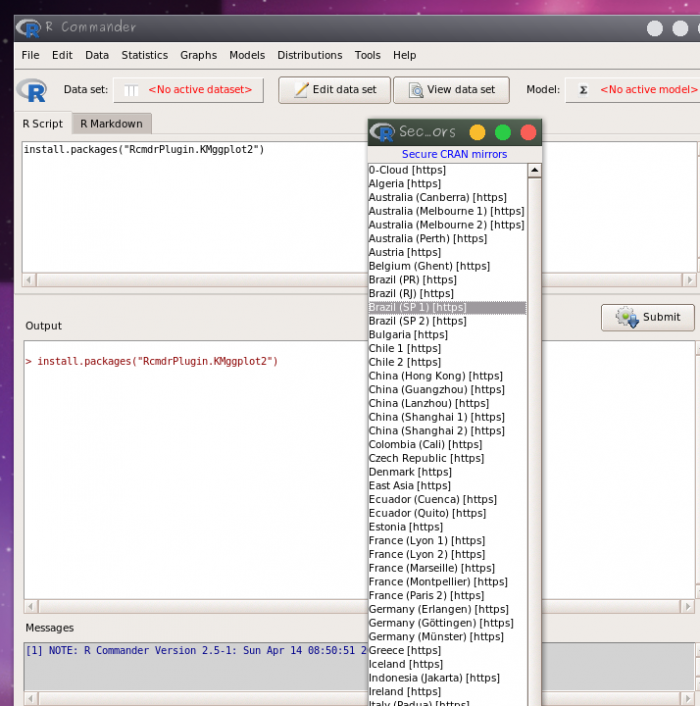
install.packages("RcmdrPlugin.KMggplot2")
Em seguida, garanta que o cursor do mouse está na linha de comando e clique no botão Submit. Na janela que ira se abrir selecione o repositório Brasil(SP1).
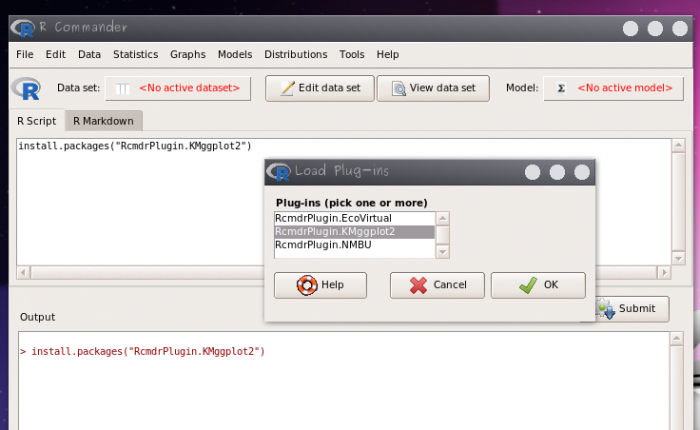
Para ativar o plugin selecione o menu Tools> Load Rcmdr plug-in(s)… e em seguida selecione o pacote RcmdrPlugin.KMggplot2.
- clique em sim na janela que solicita a reinicialização do Rcmdr
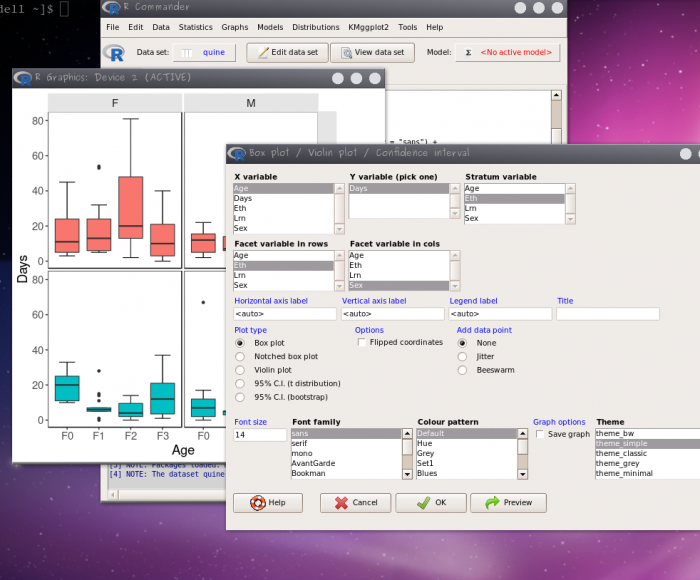
- clique na nova opção do menu KMggplot2 > BoxPlot/… e selecione as variáveis
Ajustando o GLM: dias fora da escola
Atividade
Para nosso exercício vamos deixar de lado a variável Lrn por que há dados faltantes nela com relação a outras variáveis. Vamos construir o modelo cheio com a variável resposta Days e com as variáveis preditoras (Eth, Sex, Age ) e todas as possibilidades de interações entre elas. Como estamos tratando de uma variável de contagem podemos partir direto para um modelo GLM indicando a família de distribuição de resíduos POISSON e a função de ligação log.
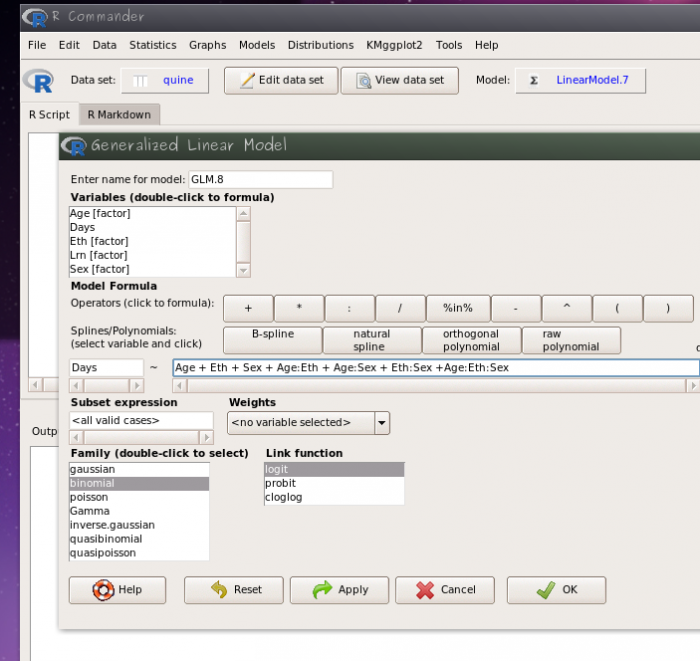
- abra o menu Statistics > Fit model > Generalized Linear Model
- construa um modelo cheio com (Age, Eth e Sex) e as suas interações possíveis:
Days ~ Eth + Sex + Age + Eth:Sex + Eth:Age + Sex:Age + Eth:Sex:Age
- faça a simplificação do modelo para reduzir o modelo ao mínimo adequado
Diagnóstico do modelo
Um dos pressupostos do modelo Poisson é que a variância aumenta linearmente com a esperança (média do modelo). Podemos avaliar isso dividindo a Residual Deviance pelo seu degrees of freedom. Essa razão deve ser próxima a 1. O que não é o caso do nosso modelo. Nesses casos uma das alternativas é:
- ajustar o modelo usando Family:
quasipoisson
Ajustando o GLM com sobredispersão
- monte o modelo cheio utilizando a família
quasipoisson; - verifique se o parâmetro de dispersão compensa a razão entre
Residual deviancee os respectivosdegrees of freedom; - siga em frente simplificando o modelo para o mínimo adequado;
- o que está representado no intercepto do modelo selecionado e qual a predição de dias de aulas perdidas para esse aluno?
- faça a predição do modelo para os seguintes alunos:
- menino aborígene no ano
F2 - menino não aborígene no ano
F2 - menina aborígene no ano
F3 - menina não aborígene no ano
F3
- interprete o modelo selecionado.
Gráfico do Modelo
O gráfico do modelo pode ser obtido no Rcmdr da mesma forma indicada no modelo anterior, no menu: Models>Graphs selecione Predict effect plots… e selecione as variáveis.
Formulário de Perguntas
- Responda as perguntas do formulário