Ferramentas do usuário
Barra lateral
Essa é uma revisão anterior do documento!
Tabela de conteúdos
Modelos Generalizados: binomial
GLM: introdução
Essa introdução aos GLM é a mesma do tutorial Modelos Lineares Generalizados, caso já tenha feito, pode passar diretamente para o tópico GLM: binomial
Os modelos lineares generalizados (GLMs) são uma ampliação dos modelos lineares ordinários. Os GLM's são usados quando os resíduos (erro) do modelo apresentam distribuição diferente da normal (gaussiana). A natureza da variável resposta é uma boa indicação do tipo de distribuição de resíduos que iremos encontrar nos modelos. Por exemplos, variáveis de contagem são inteiras e apresentam os valores limitados no zero. Esse tipo de variável, em geral, tem uma distribuição de erros assimétrica para valores baixos e uma variância que aumenta com a média dos valores preditos, violando duas premissas dos modelos lineares. Os casos mais comuns de modelos generalizados são de variáveis resposta de contagem, proporção e binária, muito comum nos estudos de ecologia e evolução.
Devemos considerar os GLMs principalmente quando a variável resposta é expressa em:
- contagens simples
- contagem expressa em proporções
- número de sucesso e tentativa
- variáveis binárias (ex. morto x vivo)
- tempo para o evento ocorrer (modelos de sobrevivência)
GLM: componentes
Uma das formas de entendermos os modelos generalizados é separar o modelo em dois componentes: a relação determinística entre as variáveis (resposta e preditora) e o componente aleatório dos resíduos (distribuição dos erros). Em um modelo linear ordinário a relação entre as variáveis é uma proporção constante, o que define uma relação funcional de uma reta. Quando temos uma contagem, essa relação pode ter uma estrutura funcional de uma exponencial. Para esses casos, os modelos generalizados utilizam uma função de ligação log para linearizar a relação determinística entre as variáveis. Portanto, a estrutura determinística dos modelos GLM's é definida por um preditor linear, associada à função de ligação.
O componente aleatório dos resíduos, no caso de uma variável de contagem, segue, em geral, uma distribuição poisson. A distribuição poisson é uma variável aleatória definida por apenas um parâmetro ($\lambda$), equivalente à média, chamada de lambda. A distribuição poisson tem uma característica interessante, seu desvio padrão é igual à média. Portanto, se a média aumenta, o desvio acompanha esse aumento e a distribuição passa a ter um maior espalhamento.
Preditor linear e função de ligação
O preditor linear está associado à estrutura determinística do modelo e está relacionado à linearização da relação, aqui definido como $\eta$:
$$ \eta = \alpha + \beta x$$
A função de ligação é o que relaciona o preditor linear com a esperança do modelo:
$$ \eta = g^{-1}(E_{(y)}) $$
Ou seja, nos modelos generalizados não é a variável resposta que tem uma relação linear com a preditora, e sim o preditor linear que tem uma relação linear com as preditoras.
Funções de ligações canônicas
Para alguns tipos de famílias de variáveis temos funções de ligações padrões. As mais usadas são:
| Natureza da resposta | Estrutura dos resíduos (erro) | Função de ligação |
|---|---|---|
| contínua | normal | identidade |
| contagem | poisson | log |
| proporção | binomial | logit |
GLM: binomial
Os modelos de proporção de sucessos (sucessos/tentativas), proporção simple (%) ou de resposta binária (presença/ausência, vivo/morto) são modelados, normalmente, com estrutura do erro binomial. Nesses casos os limites dos valores da variável resposta é bem definido: entre 0 e 1. Além disso, a variância não é constante e varia conforme a média. Essas características fazem com que os resíduos apresentem uma estrutura que aumenta e depois diminuí, e normalmente o máximo de desvios é encontrado nos valores intermediários.
Função de ligação
A estrutura da função de ligação é a mesma para qualquer modelo:
O preditor linear está associado à estrutura determinística do modelo e relacionado à linearização da relação, aqui definido como $\eta$:
$$ \eta = \alpha + \beta x$$
A função de ligação é o que relaciona o preditor linear com a esperança do modelo:
$$ \eta = g(E_{(y)}) $$
A função de ligação $g()$ para modelos com resposta binária ou proporção é chamada de logit ou log odds1), definida como:
$$ \eta = \log(\frac{p}{1-(\p)})$$
Para reverter o preditor linear da função logit para a escala de observação usa-se a função inversa:
$$ "logit"^{-1} = \frac{e^{\eta}}{(1+ e^{\eta})} $$
Resposta: proporções
Exemplo: floração
 Mais um exemplo apresentado no livro do Michael Crawley, The R Book.
Neste experimento o objetivo foi avaliar a floração de 5 variedades de plantas tratadas com hormônios de crescimento (6 concentrações). Depois de seis semanas as plantas foram classificadas em floridas ou vegetativas.
Mais um exemplo apresentado no livro do Michael Crawley, The R Book.
Neste experimento o objetivo foi avaliar a floração de 5 variedades de plantas tratadas com hormônios de crescimento (6 concentrações). Depois de seis semanas as plantas foram classificadas em floridas ou vegetativas.
Conjunto de Dados: flowering.txt
- flowered: número de plantas que floresceram
- number: número de plantas acompanhadas
- dose: concentração da dose de hormônio
- variety: variedade da planta (categórica 5 níveis)
Hipótese
O objetivo do estudo que gerou esses dados é saber se o evento de floração é influenciado pelo dose de hormônio e a variedade da planta.
- baixe o arquivo flowering.txt
- abra os dados no Rcmdr (a separação de campo é espaço) com o nome
flower - crie a variável
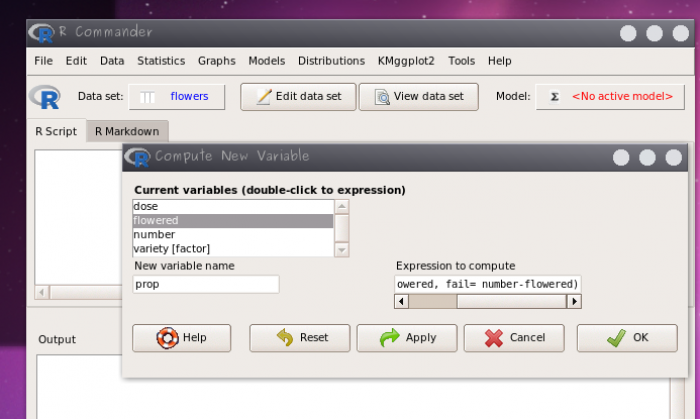
proppelo menu Data> Manage variables in active data set> Compute new variable…, colocando no campo Expression to compute:
cbind(sucess = flowered, fail = number - flowered)
Esse comando acima cria uma nova variável nos dados flower chamada prop. Essa nova variável tem duas colunas (sucess e fail) contendo o número de plantas floridas e o número de plantas que não floresceram, respectivamente.
- use a variável
propcomo resposta (sucessos, falhas) - monte o modelo cheio com todas a variáveis preditoras e interações
- simplifique o modelo para o mínimo adequado
Use os mesmos passos do modelo anterior no Rcmdr
- lembre-se que a
familynesse caso ébinomial - o procedimento para a sobre-dispersão é o mesmo que no exemplo anterior
Interpretação do resultado
Para interpretar tanto os coeficientes quanto os valores previsto é necessário aplicar a função inversa do logit, ou seja, nosso modelo faz previsões na escala de log(odds-ratio), nosso preditor linear $\eta$, e precisamos retornar para a escala de observação que é a probabilidade de florescer ($\hat{y}$):
$$\hat{y} = \frac{e^{\hat{\eta}}}{1+e^{\hat{\eta}}} $$
- calcule o predito pelo modelo e os coeficientes na escala original
- interprete o efeito da concentração na floração das variedades
Transformar os coeficientes e valores preditos pelo GLM:
Para transformar o valor predito pelo modelo (log(odds-ratio)) na escala de medida (proporção) é preciso transformar os preditos pelo modelo. Para predizer na escala de medida usamos a função predict, como no código abaixo. O predito pelo modelo, está na escala do preditor linear, portanto devemos transformar essa medida com a função inversa da logit, como no código abaixo. Lembre-se de mudar, no código, o “nomedomodelo” pelo nome que usou quando construiu o glm.
(preditoLinear <- predict("nomedomodelo"))
(preditoProp <- exp(preditoLinear)/(1+ exp(preditoLinear)))
A própria função predict, também faz o serviço completo se colocarmos o argumento type=“response”, como abaixo:
predito <- predict("nomedomodelo", type = "response")
predito
Gráfico e interpretação dos resultados
Para um gráfico dos resultados use o menu:
Models > Graphs > Predict effect plots…
A partir dos gráficos e do modelo selecionado faça um relato (5 linhas) das interpretações biológicos. Esse relato, junto ao resultado e gráficos, deve ser enviado aos professores ao final da atividade.
Resposta: binária
Exemplo: pássaro na ilha
O conjunto de dados que vamos usar, isolation.txt tem como variável:
Conjunto de dados: isolation.txt
- incidence: presença/ausência da espécie de ave (reprodução)
- area: área total da ilha ($km^2$)
- isolation: distância do continente (km)
Hipótese
O objetivo do estudo que gerou esses dados é saber se a ocorrência da ave (reprodução) está relacionada com o isolamento e tamanho da ilha.
- abra os dados
isolation.txtno Rcmdr (a separação de campo é espaço) - monte o modelo cheio com todas a variáveis preditoras e interações
- simplifique o modelo para o mínimo adequado
Use os mesmos passos do modelo anterior no Rcmdr
- lembre-se que a
familynesse caso ébinomial - o procedimento para a sobre-dispersão é o mesmo que no exemplo anterior
Interpretação do resultado
O modelo prevê a ocorrência da ave na escala de logaritmo da chance (log odds-ratio). Para interpretar tanto os coeficientes quanto os valores previsto é necessário aplicar a função inversa do logit, como no exercício anterior:
- calcule o predito pelo modelo e os coeficientes na escala original
- interprete o efeito do tamanho e distância na ocorrência da espécie
O que deve entregar?
Para cada exercício feito, deve ser entregue, em um único arquivo:
- o resultado do modelo mínimo adequado
- os coeficientes estimados, na escala de observação
- gráficos que apresentem os resultados principais
- um relato de no máximo 5 linhas, ou em tópicos, da interpretação biológica dos resultados
Sobredispersão e acumulo de zeros
Os modelo GLM poisson e binomial apresentam a variância acoplada à média dos valores, diferentemente dos modelos com distribuição normal onde a média e a variância são idependentes. Caso haja uma variação maior ou menor nos dados do que o previsto por essas distribuições, o modelo não consegue dar conta. Essa sobre-dispersão ou sub-dispersão dos dados indica que temos mais ou menos variação do que é predito pelos modelos. Isso pode ser decorrência de vários fontes de erro na definição do modelo, alguns exemplos são:
- o resíduo dos dados pode não ter sido gerado por um processo aleatório poisson ou binomial
- há mais variação do que predito pela ausência de preditoras importantes
- muitos zeros, além do predito pelas distribuições, em decorrência de diferentes processos: um que gera a ausência e outro que gera a variação nas ocorrências de sucesso
Soluções para a sobre-dispersão e acumulo de zeros
A solução mais simples para lidar com sobre-dispersão são os modelo quasipoisson e quasibinomial, que estimam um parâmetro a mais, relacionando a média à variância, o parâmetro de dispersão. Entretanto, os modelos quasi dão conta apenas de sobre-dispersões moderadas e não indicam qual a fonte dela.
Há algumas alternativas ao modelo quasi para a sobre-dispersão dos dados, alguns deles estão listados abaixo:
- modelo binomial negativo
- modelo de mistura, considerando dois processos distintos
- modelos mistos, considerando a ausência de independência das observações
- modelos com acúmulos de zeros (Zero Inflated Models).
Não é objetivo deste curso mostrar todas essas alternativas, mas caso se deparem com esse problema, muito frequente na área da biológica, saibam que existem alternativas robustas para solucioná-lo.